למת החמישה

במתמטיקה, ובמיוחד באלגברה הומולוגית וביישומים אחרים של התורה של קטגוריות אבליות, למת החמישה היא למה בעלת חשיבות בנוגע לדיאגרמות קומוטטיביות. למת החמישה תקפה לא רק בקטגוריות אבליות אלא למשל גם בקטגוריית החבורות.

נוסח פורמלי

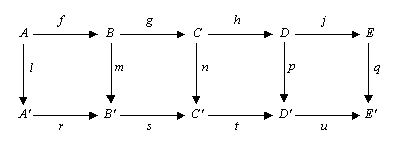
נניח כי נתונה הדיאגרמה הקומוטטיבית הבאה בקטגוריה אבלית כלשהי (או לחלופין בקטגוריית החבורות):

קובץ:FiveLemma.png

למת החמישה טוענת כי אם השורות בדיאגרמה זו הן מדויקות, ואם m ו-p הם איזומורפיזמים, l הוא אפימורפיזם ו-q הוא מונומורפיזם, אזי גם n הוא איזומורפיזם.

למת החמישה נובעת מידית מזוג למות הדואליות זו לזו הנקראות למות הארבעה. ניסוחן של למות הארבעה:

הלמה הראשונה: נניח כי השורות בדיאגרמה הקומוטטיבית הבאה מדויקות:

קובץ:FourLemma01.png

וכי m ו-p הם אפימורפיזמים ו-q הוא מונומורפיזם, אזי n הוא אפימורפיזם.

הלמה השנייה: נניח כי השורות בדיאגרמה הקומוטטיבית הבאה מדויקות:

קובץ:FourLemma02.png

וכי m ו-p הם מונומורפיזמים ו-l הוא אפימורפיזם, אזי n הוא מונומורפיזם.

הוכחה

הוכחת למות מסוג זה נעשית על ידי מרדף דיאגרמות: מעבר של איברים בדיאגרמה בעזרת מורפיזמים, תוך שימוש בתכונות שלהם. זוהי שיטה נוחה להוכחת טענות כלליות בתורת הקטגוריות, התלויות בתכונות שונות של מורפיזמים. ההוכחה עצמה לרוב טריוויאלית ומשתמשת כמעט ישירות בהגדרות.

הלמה הראשונה

כדי להוכיח ש-n הוא על, נניח ש- $a_{1} \in C^{'}$ . נסמן $a_{2} = t (a_{1})$ . השורה התחתונה מדויקת ו- $a_{2} \in I m (t)$ , ולכן $u (a_{2}) = 0$ . נתון ש- $p$ על, לכן יש $a_{3} \in D$ כך ש- $p (a_{3}) = a_{2}$ , ונסמן $a_{4} = j (a_{3}) \in E$ . לכן, לפי התחלפות הריבוע הימני נקבל $q (a_{4}) = 0$ , ומכך ש- $q$ חח"ע נקבל $a_{4} = 0$ . השורה העליונה מדויקת, לכן יש $a_{5} \in C$ כך ש- $h (a_{5}) = a_{3}$ , ונסמן $a_{6} = n (a_{5}) \in C^{'}$ (שימו לב שלא נובע ש- $n (a_{5}) = a_{1}$ !). כעת, לפי התחלפות הריבוע האמצעי, נקבל כי $t (a_{6}) = a_{2} = t (a_{1})$ , ומכך ש- $t$ הומומורפיזם נובע $t (a_{1} - a_{6}) = 0$ . מדויק השורה התחתונה, נובע שקיים $a_{7} \in B^{'}$ כך ש- $s (a_{7}) = a_{1} - a_{6}$ . נתון ש- $m$ על, ולכן יש $a_{8} \in B$ כך ש- $m (a_{8}) = a_{7}$ . נסמן $a_{9} = g (a_{8}) \in C$ . לבסוף, לפי התחלפות הריבוע השמאלי $n (a_{9}) = s (a_{7}) = a_{1} - a_{6}$ . בסך הכל, שני האיברים $a_{1} - a_{6}, a_{6} \in C^{'}$ שניהם מתקבלים בתמונת $n$ , ולכם גם סכומם (מפורשות, $n (a_{9} + a_{5}) = a_{1}$ ).

אפשר לשים לב שבאף מקום בהוכחה אין שימוש בחילופיות הפעולה (סמנטית, אפשר לכתוב אותם הוכחות עם פעולת כפל במקום חיבור).

ההוכחה על הדיאגרמה:

קובץ:FourLemma01 proof.png

הלמה השנייה

התמלול וההוכחה המלאה היא בדומה לעיל. ההוכחה על הדיאגרמה:

קובץ:FourLemma02 proof.png

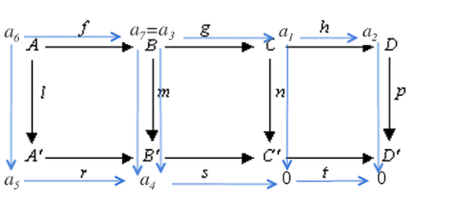
בסוף ההוכחה, מכך ש- $m$ חח"ע נובע ש- $a_{3} = a_{7}$ , ולכן לפי דיוק השורה העליונה $a_{1} = 0$ .

ראו גם

למת הנחש

קישורים חיצוניים

למת החמישה, באתר MathWorld (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

למת החמישה25204861Q1479523

למת החמישה

תוכן עניינים

נוסח פורמלי

הוכחה

הלמה הראשונה

הלמה השנייה

ראו גם

קישורים חיצוניים

תפריט ניווט

למת החמישה

נוסח פורמלי

הוכחה

הלמה הראשונה

הלמה השנייה

ראו גם

קישורים חיצוניים

תפריט ניווט

חיפוש