חזקה של נקודה
בגאומטריה, חזקה של נקודה ביחס למעגל נתון בעל רדיוס היא הגודל , כאשר הוא מרחק הנקודה ממרכז המעגל.
החזקה מוגדרת כאשר הנקודה נמצאת במישור של המעגל. החזקה של נקודות הנמצאות מחוץ למעגל היא מספר חיובי, בתוכו שלילי, ועל המעגל 0.
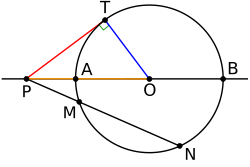
החזקה שווה למכפלת אורכי הקטעים המתקבלים מחיתוך ישר דרך הנקודה עם המעגל, כאשר מכוונים את הקטעים כראוי, ואינה תלויה בבחירת הישר. בשרטוט, החזקה היא המכפלה
המושג נטבע ונחקר על ידי יאקוב שטיינר.
הגדרות נוספות
אם הנקודה מחוץ למעגל, החזקה שלה שווה לריבוע אורך המשיק למעגל היוצא ממנה. עובדה זו נובעת ממשפט פיתגורס: משולש ישר-זווית, ולכן

אם נסתכל על המעגל במערכת צירים קרטזית כמעגל קנוני שרדיוסו , נקבל שהחזקה של נקודה היא:
מכך ניתן לראות שאם נשרטט במרחב את המקום הגאומטרי של כל הנקודות שחזקתן שווה, נקבל פרבולואיד.
שימושים
ניתן להשתמש בחזקה כדי להגדיר מקומות גאומטריים הקשורים למעגל. למשל, ציר רדיקלי הוא המקום הגאומטרי של כל הנקודות שחזקתן ביחס לשני מעגלים נתונים היא שווה.
קישורים חיצוניים
- חזקה של נקודה, באתר MathWorld (באנגלית)
- יאקוב שטיינר וחזקה של נקודה (באנגלית)







