המלון של הילברט

המלון של הילברט הוא סיפור שבו השתמש המתמטיקאי הנודע דויד הילברט בהרצאות פופולריות שנתן, והוא נועד להמחיש את התכונות המיוחדות של קבוצות אינסופיות, תכונות מפתיעות למדי למי שמורגל לעסוק רק בקבוצות סופיות.

סיפור המלון

הסיפור מדבר על בית מלון, שחדריו ממוספרים בסדר עולה: 1, 2, 3, וכו'. להבדיל ממלון רגיל, מספר החדרים במלון זה הוא אינסופי, כלומר לכל מספר טבעי קיים במלון חדר שזה מספרו (קבוצת המספרים הטבעיים היא קבוצה אינסופית ובת מנייה, כלומר ניתן למנות את אבריה לפי סדרם).

אורח חדש, ω, מגיע למלון כאשר כל החדרים במלון תפוסים. כדי לפנות לו מקום, האורח בחדר 1 עובר לחדר 2, האורח בחדר 2 עובר לחדר 3, האורח בחדר 3 עובר לחדר 4 וכך הלאה, והאורח חדש, ω, נכנס לחדר 1.

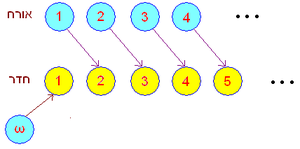
הסיפור מתחיל כאשר כל החדרים במלון תפוסים. כעת מגיע לקוח נוסף למלון ומבקש חדר. בעל המלון, שאינו מעוניין לגרום ללקוח כעס ואי נעימות, אינו אומר לו שכל החדרים תפוסים, אלא פועל על מנת לספק חדר ללקוח: הוא מבקש מהאורח בחדר 1 לעבור לחדר 2, מהאורח בחדר 2 לעבור לחדר 3, מהאורח בחדר 3 לעבור לחדר 4, וכך אורח חדר n עובר לחדר n+1, והדבר אפשרי משום שיש אינסוף חדרים. את חדר 1 שהתפנה הוא מציע ללקוח הנוסף שהגיע זה עתה.

כעת מגיעה למלון סדרה אינסופית של אורחים, אולם בעל המלון רב התושיה מצליח לשכן גם אותם: הוא מבקש מהאורח בחדר 1 לעבור לחדר 2, מהאורח בחדר 2 לעבור לחדר 4, מהאורח בחדר 3 לעבור לחדר 6 וכן הלאה. בצורה זאת, כל האורחים שהיו עד עכשיו במלון עברו לחדרים הזוגיים, ואילו את האורחים החדשים ניתן לשכן במספר האינסופי של החדרים האי-זוגיים שהתפנו.

כעת מגיעה למלון סדרה אינסופית של אוטובוסים, שבכל אחד מהם סדרה אינסופית של אורחים חדשים. אולם בעל המלון מצליח להתגבר גם על זה: ראשית, הוא מרוקן שוב את החדרים האי-זוגיים, כפי שראינו קודם. כעת, הוא משכן את כל חברי הקבוצה הראשונה בחדרים שמספרם הוא חזקה טבעית של 3, את כל חברי הקבוצה השנייה בחדרים שמספרם הוא חזקה טבעית של 5, וכן הלאה, כשהוא משתמש רק בחזקות של מספרים ראשוניים אי-זוגיים (ולכן מספרי החדרים כולם אי-זוגיים ואין התנגשות עם האורחים שכבר היו במלון). מכיוון שלכל מספר טבעי יש פירוק יחיד למספרים ראשוניים (על פי המשפט היסודי של האריתמטיקה), הרי שלא ייתכן שמספרו של חדר אחד יהיה חזקה של שני מספרים ראשוניים שונים, ולכן השיכון של האורחים במלון מבטיח שלכל אחד יהיה חדר משלו.

גרסה מעט שונה לסיפור האחרון מתארת סדרה אינסופית של אוטובוסים, שהראשון מגיע בשעה 23:00 (שעה לפני חצות), השני מגיע בשעה 23:30 (חצי שעה לפני חצות), השלישי מגיע בשעה 23:45 (רבע שעה לפני חצות), וכן הלאה - כל אוטובוס מגיע במחצית מהזמן שנותר עד חצות. בכל פעם שמגיע אוטובוס חדש, בעל המלון מעביר את כל האורחים הנוכחיים במלון לחדרים הזוגיים, ומשכן את האורחים החדשים בחדרים האי-זוגיים.

בשעה חצות בדיוק עובר בעל המלון בין החדרים כדי לראות מי נמצא בכל חדר. לתדהמתו הוא מגלה שכל החדרים ריקים. כל אורח שהיה בחדר כלשהו (n) שעה אחת לפני חצות, פינה את החדר חצי שעה לפני חצות; כל אורח שהיה שם חצי שעה לפני חצות, פינה את החדר רבע שעה לפני חצות; וכן הלאה. כלומר, כל אורח שהיה בחדר מתישהו, בזמן x לפני חצות, פינה את החדר בזמן x/2 לפני חצות; אף אורח לא נשאר בחדר.

על אף שהגיעו למלון אינסוף קבוצות של אינסוף אנשים, כל החדרים במלון ריקים! להסבר של תופעה זו, ראו הערך גבול.

פירושו המתמטי של הסיפור

הילברט בא לתאר בסיפור זה את הדרך הלא-אינטואיטיבית שבה מתנהג האינסוף בתורת הקבוצות. ה"מלון" שלו הוא קבוצת המספרים הטבעיים, שעוצמתה מסומנת $\aleph _{0}$ (קרי: אָלֶף אֶפֶס). כל אחד משלושת המקרים מראה כיצד פעולה אריתמטית מסוימת על העוצמה (כלומר, על גודל הקבוצה) משאירה אותה ללא שינוי. בין הקבוצה שמתקבלת (כל האורחים הקיימים, כולל האורחים החדשים) ובין המספרים הטבעיים (חדרי המלון) קיימת התאמה חד-חד ערכית ועל - ועל כן הקבוצות שקולות, ועוצמתן זהה.

• במקרה הראשון מתווסף אורח אחד, ולכן קבוצת כל אורחי המלון היא $\aleph _{0}+1$. הילברט משתמש בפונקציה $\!\,f(x)=x+1$ בין קבוצת האורחים (אם נניח שהאורח החדש ממסופר 0) ובין קבוצת החדרים. מכאן עולה כי $\aleph _{0}+1=\aleph _{0}$. יתרה מזו, למעשה מתקיים $\aleph _{0}+n=\aleph _{0}$ לכל מספר טבעי $\ n$. הדבר שקול לאמירה "אם מוסיפים איבר נוסף לקבוצת המספרים הטבעיים, מתקבלת קבוצה בעלת אותה עוצמה".
• במקרה השני מתווסף מספר בן מנייה ($\aleph _{0}$) של אורחים חדשים. ההתאמה של הילברט במקרה זה מראה כי $\aleph _{0}+\aleph _{0}=\aleph _{0}$. הדבר שקול לאמירה "עוצמת האיחוד של שני עותקים של המספרים הטבעיים (כגון, לבן ושחור) שווה לזו של המספרים הטבעיים עצמם".
• במקרה השלישי מתווסף מספר בן מנייה המוכפל במספר בן מנייה של אורחים חדשים, והילברט מראה כי $\aleph _{0}+\aleph _{0}\times \aleph _{0}=\aleph _{0}$.

בעל המלון אינו כל יכול - אם למלון הייתה מגיעה קבוצת אורחים שעוצמתה היא עוצמת הרצף, כלומר עוצמת המספרים הממשיים, הוא לא היה מצליח לשכן אותם. עוצמת הרצף גדולה מאלף אפס ולכן אין דרך להתאים חדר שונה לכל אורח.

העיסוק בקבוצות אינסופיות ובתכונותיהן נוגדות האינטואיציה הוא תרומתו של גאורג קנטור להתפתחות המתמטיקה. רעיונותיו של קנטור עוררו חשדנות, ואף עוינות, בקרב מתמטיקאים רבים, ורק בערוב ימיו הוכרה תרומתו האדירה למתמטיקה. על תרומה זו אמר הילברט: "אף אחד לא יגרש אותנו מגן העדן שקנטור יצר".

הרחבה אפשרית

בעיה נוספת שיכולה להתייצב בפני בעל המלון היא קבוצה אינסופית של אנשים, שמבקשת חדר לכל תת-קבוצה. כלומר שלושת האנשים הראשונים רוצים חדר לעצמם, כך גם ארבעת האנשים הראשונים, וכן כל האנשים הזוגיים רוצים גם הם חדר לעצמם. על בעיה זו בעל המלון כבר לא יוכל להתגבר. ניתן להראות זאת על ידי השאלה האם בחדר מספר X נמצא אדם שמספרו גם-כן X. ולהמשיך עם הפרכה דומה להוכחה של קנטור ש $|P(A)|\neq |A|$.

בעקבות הילברט

בסיפורים אחדים מוצג הרעיון של המלון של הילברט, ובהם:

• סיפור מאת סופר המדע הבדיוני הנודע סטניסלב לם. הסיפור מופיע בספרים:
  • Stories About Sets שבעריכת N.Ya. Vilenkin
  • Imaginary Numbers: An Anthology of Marvelous Mathematical Stories, Diversions, Poems, and Musings שבעריכת William Frucht.
• הסיפור "אור לבן" (White Light) מאת רודי ראקר
• הסיפור "אדוות בים דיראק" (Ripples in the Dirac Sea) מאת ג'פרי לנדיס זכה בפרס נבולה.
• ספרו של פיטר הוג "חוש השלג של העלמה סמילה".
• ואריציה הומוריסטית למלון של הילברט מופיעה בספר "אינסוף - המסע שאינו נגמר" מאת ד"ר חיים שפירא.

הופקו גם שני סרטי קולנוע העוסקים במלון של הילברט:

• הסרט Hotel Hilbert משנת 1996, בבימויה של קרולין רוס-פירי.
• הסרט Hotel Infinity משנת 2004, בבימויה של אמנדה בויל, שגם כתבה את התסריט.

קישורים חיצוניים

• גדי אלכסנדרוביץ', המלון של הילברט, באתר "לא מדויק", 8 בנובמבר 2010
• עוצמה - מה זה?, באתר מחוֹנ-net של משרד החינוך
• סרטון של TED Ed שממחיש את המשל באמצעות אנימציה, The Infinite Hotel Paradox - Jeff Dekofsky, סרטון באתר יוטיוב

• Steven Strogatz, The Hilbert Hotel, NY Times, May 9, 2010
• Nancy Casey, Welcome to the Hotel Infinity!
• Hilbert's Infinite Hotel, h2g2
• Hilbert infinite hotel. M. Hazewinkel. Encyclopedia of Mathematics, Springer. Accessed May 25, 2007.
• Dinosaur Comics

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0