גשר בראוני

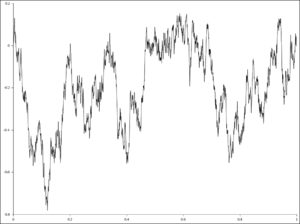
גשר בראוני הוא תהליך וינר הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle W(t)} על קטע הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,1]} בהינתן $W(1)=0$.

גשר בראוני הוא תהליך סטוכסטי רציף הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(t)} על קטע $[0,1]$ כך שלכל לכל $t$ בקטע יש לו התפלגות של תהליך וינר סטנדרטי הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle W(t)} המותנית בכך ש- $W(1)=0$. כתוצאה מכך הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(1)=0} ומתקיים גם ש-הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(0)=0} כמעט בוודאות.

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

נסמן באופן שקול:

הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(t):=(W(t)\mid W(1)=0),\;t\in [0,1]}

התוחלת של הגשר בכל $t$ במרווח $[0,1]$ היא אפס והשונות היא $t(1-t)$. לכן, השונות הכי גדולה היא באמצע הקטע ושווה לאפס בקצוות. השונות המשותפת של $B(s)$ ו- $B(t)$ היא $\min(s,t)-st$. בניגוד לתהליך וינר, התהליך אינו קבוע בזמן ותוספות זרות בגשר בראוני אינן בלתי תלויות.

גשר בראוני הוא תוצאה של משפט דונסקר בתחום התהליכים אמפיריים . הוא משמש גם במבחן קולמוגורוב-סמירנוב בתחום ההסקה הסטטיסטית.

ייצוגים נוספים של גשר בראוני

אם $W(t)$ הוא תהליך וינר סטנדרטי אז התהליך:

הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(t)=W(t)-tW(1)}

הוא גשר בראוני ומתקיימת אי-תלות בין $B(t)$ ו- $W(t)$.

באופן שקול, אם $B(t)$ הוא גשר בראוני ו- $Z$ הוא משתנה מקרי נורמלי סטנדרטי בלתי תלוי ב- $B$, אז התהליך

$W(t)=B(t)+tZ$

הוא תהליך וינר.

ניתן לייצג גשר בראוני כטור פורייה עם מקדמים סטוכסטיים:

הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle B(t)=\sum _{k=1}^{\infty }Z_{k}{\frac {{\sqrt {2}}\sin(k\pi t)}{k\pi }}}

כאשר הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle Z_{1},Z_{2},\ldots } הם משתנים מקריים נורמליים סטנדרטיים בלתי תלויים ושווי התפלגות (ראו משפט קוסמבי-קרהונן-לואב ).

קישורים חיצוניים

מדיה וקבצים בנושא גשר בראוני בוויקישיתוף

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

גשר בראוני38765971Q628309