תכנות לוגי

תכנות לוגי הוא פרדיגמת תכנות השמה דגש על יחסים ככלי הפשטה עיקרי. יחסים הם כלי המאפשר לקשר בין ערכים שונים באמצעות עובדות המוגדרות מראש.

תכנות לוגי מבוסס על תחשיב הפרדיקטים ושונה מפרדיגמות התכנות המקובלות, המבוססות על ארכיטקטורת פון נוימן. התכנות הלוגי מבוסס בראשיתו על האקסיומה: $A\quad if\quad B_{1}\land B_{2}\land ...B_{n}$. רוברט קוואלסקי הסיק שאקסיומה זו יכולה להיקרא כפרוצדורה רקורסיבית, כך ש A הוא הראש של הפונקציה וכל $B_{i}$ הוא חלק מהגוף. כלומר, כדי לפתור (להריץ) את A, יש לפתור (להריץ) את $B_{1}\land B_{2}\land ...B_{n}$.

היסטוריה

התכנות הלוגי במובן הכללי שלו, נתן בתחילה מקום למספר מימושים, כגון אלו של פישר בלאק (1964), ג'יימס סלייגל (1965), וקורדל גרין (1969). מימושים אלו היו בעצם מערכות ל"פתירת שאילתות" כמו ה Advice Taker שהוצג במאמרו של ג'ון מקארטי (1958). למרות זאת, רק ב-1969, אבסיס, שנכתבה על ידי פוסטר ואלקוק, הייתה לשפה הראשונה שעסקה בתכנות לוגי והוכרזה כשפת תכנות.

במובן הצר יותר של התכנות הלוגי, ניתן למצוא אותו כבר בדיונים הראשונים על בינה מלאכותית בסוף שנות ה-60 ותחילת ה-70. אף על פי שהייתה אכן מבוססת על לוגיקה, פלאנר, אשר פותחה ב MIT הייתה השפה הלוגית הראשונה שנבנתה על פרדיגמת התכנות הפרוצדורלי. המימוש הידוע ביותר של הפלאנר הוא המיקרו-פלאנר שנבנה על ידי ג'רי סוסמן, אגווין חארניאק, וטרי וינוגרד. השימוש בו היה למימוש השפה הטבעית של וינוגרד, והבנתה של תוכנת SHRDLU, דברים אשר היוו התקדמות רצינית ביותר באותה התקופה. מפלאנר עצמה התפתחו בנוסף גם השפות QA-4, POPLER, Conniver, QLISP, ETHER.
הייס וקוואלסקי, גם הם ניסו לקבל את גישת ההכרזה הלוגית לייצוג מידע שהוצגה על ידי פלאנר בצורתה הפרוצדורלית. הייס (1973), פיתח שפת משוואות, GOLUX, שבה ניתן לקבל פרוצדורות שונות באמצעות שינוי של אלגוריתם מציאת הפתרון לשאילתות. קוואלסקי לעומת זאת הראה כיצד ניתן לפתור באמצעות פתרון רדוקטיבי של SL-resolution את השאילתות המוצגות. לבסוף קוואלסקי, בשיתוף עם קולמיראור בעצם בנו את פרולוג על בסיס רעיונות אלו. מכאן והלאה פותחו גם ALF, Godel, Fril ועוד שפות נוספות.
בשנת 1997 הוקמה ועדת "מייסדי התכנות הלוגי" שמטרתה הייתה לתת ל-15 האנשים הללו את מקומם הראוי בהיסטוריה בתור חלוצי התכנות הלוגי.

מאפייני שפה

בתכנות לוגי אין חישוב של ערכים או טיפוסים הניתנים להם. שיטת החישוב של התכנות הלוגי היא שיטה של האחדה ומענה על שאילתות באמצעות הוכחות בלבד. לתכנות הלוגי שלושה מאפיינים הייחודיים לו:

1. תחביר -

סט של עובדות, וחוקים המגדירים יחסים בבעיה המוצגת.

2. סמנטיקה -

סט של תשובות נתונות עבור שאילתה מבוקשת. אם השאילתה המבוקשת מכילה משתנים, התשובות יכילו ערכים מתאימים לפתרון השאילתה. במידה שקיימים כאלו.

3. סמנטיקת התפעול -

• הרצה היא בדיקה של שאילתה על ידי המפרש.
• הרצה היא ניסיון למצוא סט של עובדות וחוקים שיספקו את ערכי השאילתה.
• אם מדובר בשאילתה המכילה משתנים, ההרצה תנסה לתת ערכים כלשהם, מתוך התוכנית, אשר יספקו את השאילתה. אם לא ימצאו ערכים מתאימים יוחזר ערך שלילי.
• סמנטיקת התפעול של התכנות הלוגי מבוססת על שני מנגנונים:

• האחדה של תבניות (unification): מכניזם האחראי על העברת פרמטרים והתאמת סוגי משתנים.
• גישוש נסוג (Backtracking): מכניזם שתפקידו חיפוש הוכחות.

תחשיב יחסים בתכנות הלוגי (המובן הרחב)

תחביר: סמלים אטומיים: קבועים ומשתנים.

קבועים

• יחידים אשר הם תיאור של ישות או אובייקט מסוים.
• פרדיקטים אשר מתארים יחס קיים. (ישנם כמה המוכלים מראש בשפה)
• סמלים קבועים אשר מתחילים באות קטנה.

משתנים

משתנים ייוצגו באות ראשונה גדולה לדוגמה: X,Y,DingDong, TheWitchIsDead.

ביטוי

קבועים או משתנים ייחודיים נקראים ביטוי.

נוסחה אטומית

נוסחה אטומית היא אחת משניים, חוק או עובדה. הצורה הבסיסית של נוסחה אטומית היא:

predicate-symbol(term1, term2,...termn)

כל נוסחה אטומית היא פונקציה. הרצה של כל פונקציה תעשה על ידי השאילתה שתינתן.

עובדה

עובדה היא הגדרה של n אטומים כך ש n>=1 אשר עומדים ביחס מסוים. נסתכל בקטע הקוד הבא:

father(abraham, issac)

שורה זאת לוקחת את שני הקבועים (נשים לב אות קטנה בתחילת המילה) abraham, issac וקובעת שהם עומדים ביחס Father (כלומר עובדה).

father(Abraham, issac)

בניגוד לשורת הקוד הקודמת, כאן ניתן לראות, כי השם Abraham מתחיל באות גדולה ועל כן הוא משתנה. הצורות הפשוטות ביותר של עובדה הן true, false.

תבנית

לכל פרדיקט שנבנה קיימת תבנית, התבנית בנויה ממספר ביטויים ותוגדר על ידי מספר זה. לדוגמה מספר הביטויים של father שהוגדר קודם הוא 2. אם נגדיר מחדש את father עם מספר ביטויים שונה הפרדיקט לא יוגדר כאותו פרדיקט. נגדיר אותו כ father/1 father/3 father/4 וכדומה.

חוק

הגדרה של יחס בתנאי מסוים נקראת חוק. נתבונן בקטע הקוד הבא:

father(X, issac) :- X=abraham

במקרה זה נגיד כי X עומד ביחס father עם issac אמ"מ X=abraham. הפרדיקט "=", כאמור, הוא פרדיקט אשר בנוי לתוך התכנות הלוגי.
ראש החוק הוא החלק הראשון אשר מגיע לפני הסימן -: בעוד שהחלק השני הוא הגוף. הגוף יכול להיבנות באמצעות יותר מחוק אחד ולהיות מופרדת בפסיקים כמו שנראה בהמשך. כל "," כזה הוא הפרדיקט and. כלומר כדי שהראש ייתן ערך true יש לדאוג לכך שכל הערכים בגוף המופרדים בפסיקים יתנו ערך דומה.

• חוק מגדיר טווח לקסיקלי פנימי שהאברים הקשורים אליו ניתנים בראש. נשים לב שבדיקת חוק היא רקורסיבית ועל כן כאשר נגדיר משתנה חדש בתוך חוק הבדיקה תעשה בטווח חדש שניתן לאותה נוסחה אטומית שהוא קשור אליה.
• בעיסוק רקורסיבי בחוקים נשתמש הרבה בעקרון השמת שמות, כלומר לתת שם חדש למשתנה קיים. זאת מכיוון שנעבור אזורי קוד שונים וכל פעם שנכנס רמה פנימה לתוך החוק נצטרך להבדיל בין הערכים השונים הניתנים.

שאילתה

שאילתה היא בעצם בדיקה של מאגר האקסיומות שבנינו מראש. בהרצת שאילתה כלשהי ירוץ אלגוריתם שיבדוק אחד אחד בסדר כלשהו את העובדות והחוקים שניתנו בהקדם וינסה להוכיח את השאילתה.

?- father(X,Y)

שאילתה זאת תחזיר לנו X=abraham, Y=issac. המשך הרצה של השאילתה עם האקסיומה היחידה שנתנו מעוד מועד יחזיר false. זאת מאחר שאין עוד ערכים שיאמתו את השאילתה. נשים לב כי הרצה של שאילתות יכולה גם להכיל קבועים בלבד ולא משתנים ואפילו להכיל מספר ביטויים שונים להוכחה.

מוסכמות כתיבה

• הגדרת פרוצדורות תעשה בבלוק יחיד ומופרד מפרוצדורות נוספות.
• כל הגדרה של פרוצדורה תחל בחוזה אשר יתאר את חתימתה (Signature specification) ואת היחס שהיא מגדירה (Purpose declaration).
• עובדות וחוקים בהגדרת פרוצדורה יהיו ממוספרות.

המפרש

המפרש תפקידו לחשב סט של תשובות, תחלופות, עבור המשתנים הנתונים בשאילתה. כל תשובה מייצגת הוכחה של השאילתה, במידה ואין הוכחה אז הסט ריק. כל סט כזה מהווה ניסיון נוסף לפתור את השאילתה וניסיון נוסף לשימוש בחוקים למציאת ההוכחה. המפרש עובר ע"פ סדר שאינו דטרמניסטי על כל החוקים והעובדות (בפרולוג למשל הסדר הוא ע"פ סדר הכתיבה שלהם), ומחפש אלמנטים שיוכיחו את השאילתה המבוקשת. שלב זה הוא שלב הגישוש הנסוג. המפרש יתייחס לכל עובדה כאילו היא חוק בעל ערך true. אלגוריתם ההוכחה של המפרש מניח מראש כי קיים איטרטור "is" אשר עוקב אחרי הסדר של בדיקת השאילתה והחוקים והעובדות אשר נבדקו כבר.

אלגוריתם מענה על שאילתה

קלט

שאילתה- Q=?-Q1,Q2,...Qn

תוכנית- P

סט ריק - s

איטרטור- is

אלגוריתם

1. אם Q=?-true,...,true החזר את s וצא.
2. החלף את שמות המשתנים הקיימים בשמות חדשים.
3. בחר את ביטוי השאילתה הבא שערכו אינו true באמצעות האיטרטור is וקרא לו G
4. בחר את החוק הבא וקרא לו A כך ש

unify(A,G)=s2

אם נמצא החוק המתאים הרץ שאילתה חדשה ללא G עם הסט החדש ואיטרטור חדש.
5. אם ישנם עוד חוקים לאיטרטור, עבור לחוק הבא באיטרטור עם אותם הנתונים.

פלט

סט המקיים את ההוכחה או סט ריק.

עצי הוכחה

חישוב האלגוריתם של המפרש מתואר על ידי עץ הוכחה אשר מוגדר בצורה הבאה:

1. אברי העץ מכילים את השאילתות.
2. ענפיו מסומנים במספרי חוקים וחישובי האחדת תבניות.
3. איבר הבסיס של העץ הוא השאילתה לפתרון ויסומן על ידי Q. כל תת-עץ הוא דרך הוכחה של איבר הבסיס של אותו העץ.
4. ענף בעץ בעל חישובים נכונים לכל אורכו מהווה הוכחה של השאילתה. מה שהופך את העץ לעץ הצלחה.
5. אם עץ ההוכחה סופי ואין עליו מסלולי הוכחה נכונים העץ יקרא עץ כישלון סופי.
6. אם עץ ההוכחה אין סופי וקיים עליו מסלול הוכחה אמיתי כלשהו העץ יקרא עץ הצלחה אין סופי.

נתבונן בדוגמה הבאה ונבנה עץ הוכחה:

Signature: father(F,S)/1
1. father(abraham, issac).
2. father(haran, lot).
3. father(haran, yiscah).
4. father(haran, milcah).

Signature: male(P)/2
1. male(issac).
2. male(lot).

Signature: female(P)/3
1. female(milcah).
2. female(yiscah).

Signature: son(C,P)/4
1. son(X,Y) :- father(Y,X), male(X).

Signature: daughter(C,P)/5
1. daughter(X,Y) :- father(Y,X), female(X).

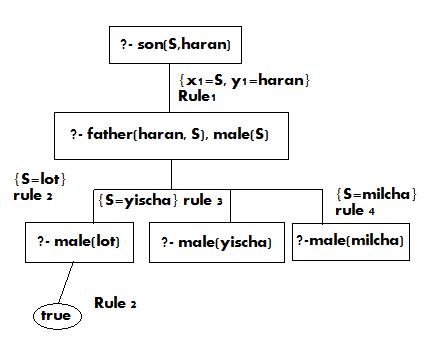
Q= ?- son(S,haran).

אמצע

כפי שניתן לראות העץ הוא עץ הצלחה, תוצאת התחלופות בענף ההצלחה היא:

{X1=S, Y1=haran}=>{S=lot} => {X1=lot, Y1=haran, S=lot}

לבסוף ההגבלה למשתני השאילתה עצמה מחזירה את התשובה, S=lot.

דטרמניסטיות בתכנות הלוגי הבנוי על תחשיב היחסים

בהינתן שאילתה Q ותוכנית P ההכרעה האם P מספק את Q היא דטרמניסטית:

עץ הוכחה בנוי ממספר איברים אשר כוללים שאילתות ונוסחאות אטומיות. הנוסחאות האטומיות מורכבות מפרדיקטים, קבועים אשר נמצאים בתוך התוכנית ובשאילתה וכמובן ממשתנים. מכאן שמספר האטומים ומספר השאילתות הקיימות הוא סופי. כלומר, המסלולים בעץ ההוכחה הם סופיים וניתן להכריע בשאלה האם P מספק את Q.

עם זאת, לא ניתן להסיק מכך שכל עצי ההוכחה סופיים. גודלו של עץ ההוכחה תלוי באלגוריתם היוצר אותו. השאלה המרכזית היא האם האלגוריתם יודע לזהות כפילויות בשאילתות שכבר נעשו בשלב מוקדם יותר, וזאת אף על פי שנעשתה החלפה בשמות המשתנים.

קישורים חיצוניים

מדיה וקבצים בנושא תכנות לוגי בוויקישיתוף

• תכנות לוגי, דף שער בספרייה הלאומית

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

35686559תכנות לוגי