קו השרשרת

דגם קו השרשרת של אנטוני גאודי בקאזה מילה, ברצלונה

במתמטיקה ופיזיקה, קו השרשרת (או עקום השרשרת) היא הצורה המתקבלת כאשר תולים כבל או שרשרת בשתי נקודות קצה, שנוסחתה הטיפוסית:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\cosh(x)=\frac{e^x+e^{-x}}{2}} (קוסינוס היפרבולי)

השפעתה האחידה של כוח הכבידה מארגנת את חוליות השרשרת בעקומה טיפוסית, שלהּ שיפוע תלול קרוב לנקודות התלייה, היכן שמשקלה המלא של השרשרת מותח אותן, ושיפוע מתון יותר לקראת אמצע השרשרת. באנגלית קרוי קו השרשרת "catenary", מן המילה הלטינית "catena", שמשמעותה "שרשרת".

צורת העקום שיוצרת שרשרת תלויה הביאה את גלילאו לשער כי מדובר בפרבולה, אך ב-1669 הראה Joachim Jungius כי פרבולה אינה מתארת את הקו במדויק. בעקבות שאלה של יאקוב ברנולי, מצאו לייבניץ, הויגנס, ויוהאן ברנולי את הפתרון, שתרם לתחילת פיתוחו של חשבון הווריאציות.

זוהי העקומה הממזערת את האנרגיה הפוטנציאלית הכוללת של השרשרת, בכפוף לאילוצים של נקודות הקצה, ומקטינה את כוח המתיחה הפועל על השרשרת. משום כך, משתמשים בצורה דומה גם כדי לבנות קשתות גבוהות, כדוגמת קשת השער בסנט לואיס.

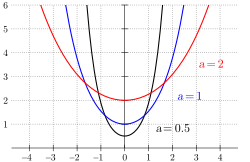
התיאורים הגרפיים משמאל הם של קווי שרשרת שונים, שנוסחתם הפרמטרית היא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=a\cosh\left(\frac{x}{a}\right)=\frac{a}{2}\bigl(e^\frac{x}{a}+e^{-\frac{x}{a}}\bigr)}