פונון

שגיאות פרמטריות בתבנית:פירוש נוסף
פרמטרי חובה [ נוכחי ] חסרים

תנודות בסריג חד ממדי באורכי גל שונים. עבור אינטראקציות בין אטומית המודל ההרמוני מתאר רק תנודות קטנות סביב מרחק שיווי המשקל, ולא כפי שמוצג באנימציה

פונון בפיזיקה הוא אופן תנודה מקוונטט המתקיים בגבישים מוצקים, ובנוזל-על של הליום 4. בעקבות האינטראקציות הבין אטומיות בגביש המוצק תזוזות האטומים מקיימות משוואת גלים, שפתרונה הוא בקירוב גל מתקדם בצורה הרמונית. מבחינה זו פונון מתאר קוואזי-חלקיק בחומר, הנושא את שדה הכוחות הבין אטומיים. מחקר הפונונים הוא חלק חשוב בפיזיקה של מצב מוצק, משום שלפונונים תפקיד חשוב בקביעת התכונות הפיזיקליות של מוצקים, ובכללן מוליכות תרמית ומוליכות חשמלית. באופן כללי, פונונים המאופיינים באורך גל גדול מהווים את גלי הקול המתפשטים במוצק, ומכאן שמם פונון, קול ביוונית. פונונים בעלי אורך-גל קצר יותר אחראיים לקיבול החום במוצקים. במבודדים תרמיים, פונונים הם גם המנגנון המרכזי המאפשר הולכת חום.

פונונים הם המקבילה הקוונטית של אופני תנודה נורמליים, הידועים גם בפיזיקה קלאסית, ומתקיימים כאשר חלקים בעצם מתנודדים באותה תדירות. לפי תוצאה ידועה של מכניקה קלאסית, תנודה נתונה כלשהי של העצם ניתנת לביטוי כסופרפוזיציה של אופני תנודה נורמליים, בתדירויות שונות. למרות שבמכניקה הקלאסית אופני תנודה הם תופעה גלית, הרי במכניקה הקוונטית מביאים בחשבון גם את התכונות החלקיקיות שלהם, ומטפלים בהם כאל חלקיקים, הקרויים פונונים.

הפונונים הם בוזונים בעלי ספין אפס.

תנודה בגביש יכולה להיווצר כתוצאה מדחיסה או מתיחה של המרחק בין אטומים שכנים, פונון כזה נקרא פונון אורכי (LA), או על ידי תזוזה בניצב לציר ההתקדמות, כעין פעולת גזירה בדומה למיתר גיטרה. פונון כזה יקרא פונון רוחבי (TA), והוא כולל שתי דרגות חופש, הפורשות את המישור הניצב להתקדמות במרחב התלת ממדי. תנודה בנוזל על נקראת רוטון, או מקסון: רוטון הוא עירור, כאשר יחס הפיזור של העירורים הייסודים מראה רגעים קרובים למינימום באנרגיה (כאשר המומנטום עולה) וכאשר המומנטום קרוב למינימום, הפונון נקרא מקסון.

בנוסף, כאשר תא היחידה הקונבנציונלי של הסריג מורכב מאטומים שונים או ממרחקים שונים בין אטומים, ייווצרו בנוסף לפונונים האקוסטיים בעלי אורכי הגל הארוכים, גם פונונים שאורך הגל שלהם הוא מסדר גודל של תא היחידה, (קרי: אטומים שכנים ינועו לכיוונים מנוגדים), שלהם תהיה אנרגיה גבוהה יותר (תנודות מהירות יותר). אופני תנודה אלו נקראים גם פונונים אופטיים, מכיוון שאפשר לעורר אותם על ידי קרינת אור (בדרך כלל בתחום התת-אדום).

פונונים אורכיים בשרשרת קפיצים חד ממדית

פונונים אקוסטיים ואופטיים בשרשרת דו-אטומית. תא היחידה כולל בתוכו שני אטומים

יחס נפיצה של פונונים אקוסטיים ואופטיים בשרשרת אטומים חד ממדית.

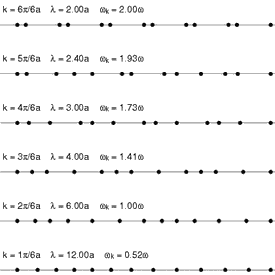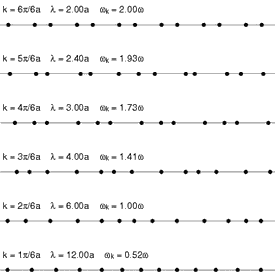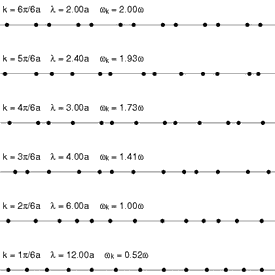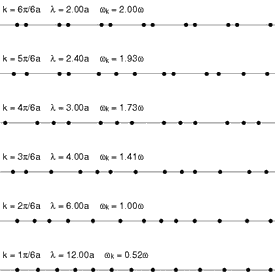
תיאור פשוט של פונונים ויחס הנפיצה שלהם ניתן לתיאור על ידי קירוב האינטראקציות הבין אטומיות למתנדים הרמוניים בין שכנים קרובים, בדומה לתגובת קפיץ למתיחה או דחיסה.

נניח שרשרת אטומים המחוברים ביניהם בקפיצים בעלי קבוע קפיץ $\ K$. נסמן את תזוזת האטום ה-$\ n$ ב $\ U_{n}(x)$.

$\cdots$------O------------O------------O------------O--------$\cdots$

$U_{n-1}\quad U_{n}\quad U_{n+1}\qquad$

משוואת הכוחות עבור החלקיק ה-$\ n$ נתונה על ידי המרחק בין החלקיק לשכניו הקרובים

$\ m{\frac {d^{2}U_{n}}{dt^{2}}}=-K\left[(U_{n}-U_{n-1})+(U_{n}-U_{n+1})\right]$

פתרון משוואה זו, בדומה למתנד הרמוני, היא גל מתקדם:

$\ U_{n}=U_{0}e^{i{\vec {k}}{\vec {a}}n-i\omega t}$

כאשר ${\vec {k}}$ הוא וקטור הגל, ${\vec {a}}$ הוא וקטור הסריג ו- $\omega$ היא תדירות הגל.

הצבה של הפתרון במשוואת הכוחות וצמצום שני האגפים משאיר אותנו עם יחס הנפיצה $\ \omega (k)$ :

$\omega ^{2}={\frac {K}{m}}\left[2-e^{i{\vec {k}}{\vec {a}}}-e^{-i{\vec {k}}{\vec {a}}}\right]=2{\frac {K}{m}}\left[1-cos(ka)\right]$

שימוש בזהות טריגונומטרית נותן לנו ביטוי מפורש יותר של יחס הנפיצה:

$\ \omega =2{\sqrt {\frac {K}{m}}}\left|sin\left({\frac {ka}{2}}\right)\right|$

אשר עבור וקטורי הגל הנמוכים (אורכי גל ארוכים), נותן יחס ליניארי בקירוב. פונונים אלה נקראים פונונים אקוסטיים (בניגוד לפונונים אופטיים), והם כאמור אחראיים לנשיאת גלי הקול בחומר המוצק.

את מהירות גלי הקול נוכל לקבל מהגדרת מהירות החבורה:

$v_{g}\equiv {\frac {\partial \omega }{\partial k}}$

שהיא מהירות התקדמות גלי הקול בתווך המוצק

$C_{s}=v_{g}={\sqrt {\frac {K}{m}}}a$

מהירות הקול בחומר מוצק היא בדרך כלל מהירה הרבה יותר ממהירות הקול באוויר. יחס הנפיצה הליניארי של גלי הקול מאפשר לקול לעבור בתווכים מוצקים מבלי להתעוות.

שרשרת דו אטומית

כאמור לעיל, שרשרת אטומית המורכבת מכמה סוגי אטומים שונים כוללת בתוך תא היחידה הקונבנציונלי יותר מאטום אחד. דבר זה מפצל את אופני התנודה של הסריג לשני ענפים - פונונים אקוסטיים, בעלי תדירות נמוכה, ופונונים אופטיים בעלי תדירות גבוהה ואורך גל קצר, שהוא מסדר הגודל של תא היחידה.

ניתן לנתח באופן דומה לזה שנעשה עבור שרשרת מונואטומית גם שרשרת בעלת שני סוגי אטומים שונים (למשל: מלח בישול NaCl). פתרון המשוואות מגלה יחס נפיצה ריבועי:

$\omega _{\pm }^{2}=K\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)\pm K{\sqrt {\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)^{2}-{\frac {4\sin ^{2}(ka/2)}{m_{1}m_{2}}}}}\,$

כאשר $m_{1}$ ו-$m_{2}$ הן מסות האטומים השונים.

פתרון המשוואה הריבועית מגלה את שני הענפים, האקוסטי והאופטי, ואת פער האנרגיה ביניהם.

ראו גם

• פוטון
• פלזמון
• רוטון

קישורים חיצוניים

מדיה וקבצים בנושא פונון בוויקישיתוף

• 
  שגיאות פרמטריות בתבנית:בריטניקה
  פרמטרי חובה [ 1 ] חסרים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32667039פונון