סריג עקיפה

סריג עקיפה (באנגלית: Diffraction Grating) באופטיקה הוא רכיב אופטי בעל תבנית מחזורית, אשר מפצל אור הפוגע בו לכיוונים שונים בתבנית מחזורית (סוג של תופעת עקיפה אופטית). הסריג יכול להיות מיועד לפעולה בהעברה או בהחזרה של האור. זווית הפיזור מהסריג תלויה במרווח הסריג ובאורך הגל של האור הפוגע, ובשל כך יש להם שימושים בספקטרוסקופיה וביצירת אור מונוכרומטי.
דוגמה לסריג עקיפה היא שקופית שעליה דוגמה עדינה של פסים שחורים או חריצים, אשר יכולה לשמש כסריג עקיפה בהעברה ובהחזרה של אור.
העקרונות של סריגי עקיפה נתגלו על ידי ג'יימס גרגורי בניסויים בנוצות ציפורים, שנה לערך אחר ניסויי הפריזמה (המנסרה) של ניוטון. הסריגים המלאכותיים הראשונים יוצרו בסביבות שנת 1785 על ידי ממציא מפילדלפיה בשם דייוויד ריטנהאוס באמצעות שערות שהונחו בין שני ברגים בעלי הברגה עדינה.

עקרון הפעולה
משוואת הסריג היא הקשר המתמטי בין מרווח הסריג , אורך הגל הפוגע וזוויות הפגיעה והפיזור מהסריג. לפי עקרון הויגנס-פרנל, כל נקודה על חזית גל מתקדם מתפקדת כמקור נקודתי, וחזית הגל בכל נקודה עוקבת תתקבל על ידי סיכום תרומות כל המקורות הנקודתיים האינדיווידואליים (בלתי-תלויים). סריגים יכולים להיות מעבירים (transmissive) או מחזירים (reflective), באנלוגיה לעדשה או מראה בהתאמה.
נתבונן בשתי קרניים סמוכות (בסריג העברה, למשל, הכוונה היא לאור שעובר דרך שני רווחים סמוכים בסריג).

לאחר שאור מבצע אינטראקציה עם הסריג, האור, אשר עבר דיפרקציה, מורכב מסכום כלל התאבכויות מרכיבי הגל הנובעים מכל חריץ וחריץ בסריג. בכל נקודה במרחב המרחק מכל חריץ בסריג משתנה. מאחר שהמרחק משתנה תשתנה גם פאזת כל גל המגיע מאחד מחריצי הסריג, כך שבנק' כללית במרחב בה יתבצע חיבור או חיסור, התאבכות בונה או הורסת, של הגלים המגיעים מחריצים שונים כתלות בפאזה. כאשר הפרש הדרכים לנק' כללית של שני חריצים סמוכים שווה לחצי אורך גל, דהיינו , הגלים אינם בפאזה אחד עם השני ותתבצע התאבכות הורסת, הגלים יבטלו אחד את השני כך שנקבל נקודה בעלת עוצמת אור מינימלית. לחלופין, בנקודה בה הפרש הדרכים הוא , נקבל התאבכות בונה, כאשר הנקודה בעלת עצמת אור מקסימלית. מעקרון זה נקבל את משוואת הסריג במקרה של זווית פגיעה ניצבת למשטח:

כאשר היא הזווית בין הקרן שעברה דיפרקציה לבין הנורמל לסריג, ו–d הוא המרחק בין מרכזי שני חריצים סמוכים, m הוא מספר שלם המייצג את סדר הדיפרקציה.
כאמור, עבור פגיעת אור נורמלית – בניצב לסריג, נקבל נקודות עצמה מקסימליות עבור המקיימות - , אך ניתן להרחיב את הכלל למקרה בו הגל פוגע בסריג בזווית כללית , ונקבל את הקשר , כלומר .
יש לציין כי עבור משוואות אלו הנחנו כי משני עברי הסריג מצוי אותו התווך (כדוגמת אוויר).
לכל m עבורו יש פתרון למשוואה תתאים זווית בה נקבל התאבכות בונה ולכן פיזור (ראה איור 2 ואיור 4, כאשר הראשון עם הזוויות המתאימות ל- m= 1, 0, -1 והשני עם הזוויות המתאימות ל-2-, m=2, 1, 0, -1).
אם אלומת אור המורכבת ממספר אורכי גל פוגעת בסריג, כמו מנורת הכספית בתמונה או אור שמש, אזי האור נשבר כך שלכל אורך גל יהיה פיזור נפרדה מתאים למשוואת הסריג.
ביטוי מתמטי לסריג ולשדה רחוק ממנו
ניתן לפתח ביטוי מתמטי לסריג עקיפה המתואר על ידי פונקציה מחזורית בתוך מפתח סופי. עבור סריג מחזורי ואינסופי הפונקציה שמתארת אותו היא אינסופית ומחזורית כך ש-. כלומר הוא המחזור של הפונקציה. ולכן ניתן להציג את הפונקציה על ידי טור פורייה:
כאשר הם מקדמי טור פורייה:
בנוסף אם הסריג הוא בעל אורך סופי, כאשר גודל המפתח הוא (ראה פונקציית מלבן), אז ניתן לייצג את הסריג ע"י:
על ידי שיקולים באופטיקת פורייה ניתן לנתח את השדה בכל נקודה – ובפרט בשדה הרחוק. התנאי לשדה הרחוק הוא כאשר מתקיים . את השדה הרחוק ננתח באמצעות קירוב פראונהופר – (ראה עקיפת פראונהופר – פירוט על תנאי לשדה רחוק וחישוב השדה הרחוק לאחר מפתח סופי). נעזר בהתמרת פורייה של המכפלה (ע"פ משפט הקונבולוציה):
בהינתן שהתמרת הפורייה של כל פונקציה בנפרד:
כאשר .
השדה הרחוק מהסריג לאחר פגיעה של השדה בעל אמפליטודה אחידה שפגע בסריג בכיוון הניצב לו (זווית הפגיעה שווה ל-0), נקבל:
כאשר C הוא קבוע שמוגדר להיות:
לכן, הביטוי הסופי לשדה הרחוק עבור שדה בפגיעה ניצבת בסריג, לאחר הצבת הוא:
הערה: עבור פגיעה לא ניצבת (פגיעה בזווית)
תחילה נתאר את השדה לאחר הפגיעה בסריג. הגל המישורי הפוגע מתואר ע"י:
ולכן השדה החשמלי מיד לאחר הפגיעה בסריג הדיפרקציה הוא:
תכונות הסריג (בפרט בשדה הרחוק)
מתוך הביטוי של השדה הרחוק מהסריג לאחר פגיע של השדה בעל אמפליטודה אחידה שפגע בסריג בכיוון הניצב לו:
ניתן לתאר מספר תכונות ע"פ עוצמת השדה הרחוק ע"פ הדיאגרמה של העוצמה כפונקציה של .
מתוארת דיאגרמה של העוצמה כפונקציה של ציר התמונה למרחק מהסריג. ניתן לראות את סדרי הדיפרקציה השונים, כאשר כל סדר דיפרקציה הוא מהצורה SINC עקב המפתח המלבני, והמרחקים בין הפיקים (העוצמה המקסימלית של כתמי האור) נקבע על ידי אורך המחזור של הסריג (זאת ע"פ הפיתוח המתמטי)


סדר דיפרקציה
ניתן לראות באיור 6 את סדר 0 שהוא צבע לבן שמכיל את כל הספקטרום, ובנוסף בסדרים האחרים המרחק מסדר 0 תלוי גם באורך הגל - וזאת מאחר שמשתמשים באור פוליכרומטי (המורכב ממספר אורכי גל שונים). כפי שניתן לראות באיור 6, במרכז מתקבל אור לבן ובסדרים הנוספים רואים את תופעה זו, כאשר המרחק מהמרכז תלוי במרחק המסך, אורך המחזור של הסריג ובאורך הגל.
נכפה על האור תנאי שפה מחזורי (פאזה ואמפליטודה), ומתקבל סכום בדיד של גלים מישוריים, כאשר כל גל הוא תלוי בסדר הדיפרקציה n. דבר זה גורם למרחקים בין כתמי אור שונים בשדה הרחוק.
המרחק הזוויתי בין סדרי הדיפרקציה
מתוך הביטוי של השדה הרחוק ניתן לראות כי המרחק בין סדר דיפרקציה n לבין המרכז (סדר 0) הוא:
כלומר המרחק בין כל סדר דיפרקציה הוא: .
לפי קירוב לזוויות קטנות נקבל כי . לכן נקבל שהמרחק הזוויתי הוא בקירוב המרחק בין סדר הדיפרקציה מהמרכז ביחס למרחק z מהסריג.
ולכן המרחק הזוויתי בין כל סדר דיפרציה הוא: .
הערה: נתייחס לתוצאה זו למשוואת הסריג שראינו בתחילת הערך. קיבלנו שמשוואת הסריג עבור פגיעה בניצב לסריג: .
ואכן, לאחר חלוקה ב-d, ניתן לראות כי מתקבל שזווית הדיפרקציה תלויה באורך הגל ביחס למחזור הסריג (או המרחק בין החריצים).
הערה: עבור פגיעה לא ניצבת
תחילה נתאר את השדה לאחר הפגיעה בסריג. הגל המישורי הפוגע מתואר ע"י:
ולכן השדה החשמלי מיד לאחר הפגיעה בסריג הדיפרקציה הוא:
בנוסף, מתקיים . לכן נקבל את המשוואה הבאה:
, וממנה נקבל כי:
.
הערה: נתייחס לתוצאה זו למשוואת הסריג שראינו בתחילת הערך. קיבלנו שמשוואת הסריג עבור פגיעה בניצב לסריג: . ואכן, לאחר חלוקה ב-d, ניתן לראות כי מתקבל שזווית הדיפרקציה תלויה באורך הגל ביחס למחזור הסריג (או המרחק בין החריצים) ובזווית הפגיעה.
הרוחב הזוויתי של כל סדר דיפרקציה
הרוחב הזוויתי נקבע ע"פ גודל המפתח. ככל שהמפתח גדול יותר נקבל נקודת אור ממוקדת יותר, ולכן עצם היותו של המפח סופי, נקבל כתם בעל רוחב מסוים. הרוחב תלוי בהתאפסות הראשונה של הפונקציה, ולכן נקבל כי הרוחב של כל סדר דיפרקציה הוא: .
ולכן הרוחב הזוויתי של כל סדר דיפרקציה הוא: .
העוצמה היחסית בין סדרי הדיפרקציה ויעילות הסדר
העוצמה היחסית היא מקדמי הסריג כפי שניתן לראות משפיע על העוצמה של כל סדר דיפרציה. היעילות מוגדרת באופן הבא:
, ומתוך הגדרת ההספק נקבל כי .
דיספרסיה של הסריג
הדיספרסיה של הסריג מוגדרת להיות , כאשר הזווית היא זווית השבירה של האור יחסית לציר האופטי (סדר 0).
עבור הדוגמה הקודם למשל, אם המרחק הזוויתי הוא , אז נקבל כי הדיספרסיה של הסריג היא: .
כושר ההפרדה של הסריג (resolving power)
כושר ההפרדה הספקטרלי של סריג מוגדר כ-, כאשר , , ובשדה הרחוק האפס הראשון של סדר הדיפרקציה של אורך גל מסוים הוא בדיוק במקום שבו סדר הדיפרקציה של אורך גל אחר במקסימום.
עבור מפתח ברוחב , ומחזור הסריג הוא , ונגדיר את מספר המחזורים: .
ולאחר פיתוח, נקבל שכושר ההפרדה הוא:
.
סריג עקיפה כמנסרה
בתת נושא זה נראה כיצד ניתן ליצור סריג המתנהג כמנסרה (פריזמה) (כפי שניתן לראות באיור 8).
פריזמה, ראה מנסרה (אופטיקה), היא רכיב אופטי המשמש לשבירת והחזרת קרני אור ולעיתים גם לפירוק האור לספקטרום אורכי הגל השונים שלו. נבחין כי המנסרה שולחת את קרני האור בהטייה מסוימת ביחס לזווית הפגיעה (כפי שמשורטט באיור 7), כאשר השינוי בזווית נובע מהחומר (מקדם השבירה), אורך הגל של האור והצורה הגאומטרית.

המנסרה (מנסרה משלושת – כדוגמה), גורמת להטייה בזווית, כפי שניתן לראות.
ניתן לאפיין את המנסרה כאשר הקרן שהולכת בכיוון זווית ההטייה (באזור 2) הוא הסדר היחיד של הרכיב. אמנם יש התפצלות של האור לפי אורך הגל, אבל כל אורכי הגל סביב זווית זו. בהשוואה לסריג עקיפה, ניתן להבחין כי ניתן לבנות את הסריג בצורה כזו שרק סדר 1 קיים ושאר הסדרים התאפסו.
כלומר אם נחזור לטור פורייה שמייצג את הסריג, נרצה שהמקדם עבור n=1 יהיה שווה ל-1, וכל השאר 0. כלומר נבנה סריג עקיפה כך שפונקציית הסריג היא איבר יחיד מטור פורייה:

.
נבחין כי הפאזה ליניארית ב- והערכים הם מ-0 עד במחזוריות של . כלומר צבירת הפאזה כפונקציה של המקום נראית כך:

כלומר עלינו לבנות סריג מחזורי, כאשר בכל מחזור יש משולש, כאשר ניתן לתכנן אותו ע"פ אורך גל מסוים.
עבור משולש מסוים ניתן לחשב את הפאזה שהשדה צובר – כלומר את עומק הסריג, כאשר (מקדם השבירה של החומר):
. ניתן לראות הסבר גרפי באיור 9.
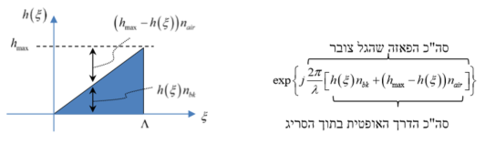
על-מנת שהסריג יתנהג כמנסרה (סדר 1 בלבד, כפי שניתן לראות באיור 8), נשווה בין הפאזה הנצברת לפאזה של סדר 1 (ללא התרומה של הפאזה הקבועה):
ולכן, כדי לקבל סריג עם סדר 1 בלבד, נתכנן את המשולש כצבירת פאזה ליניארית, כך ש:
,
מאפנן אקוסטו-אופטי
מאפנן אקוסטו-אופטי הוא מאפנן חד-ממדי. עקרון הפעולה הוא שיוצרים גל אקוסטי בתוך גביש שקוף. במקומות שבהם הגל עובר הוא יוצר שינוי קל של מקדם השבירה - וזה האיפנון. לכן אם נשדר גל אקוסטי בתדר הוא יתקדם בגביש ויצור הפרעה מחזורית בתדר מרחבי.
מניחים הוא בתדר של RF. המהירות של גל האקוסטי היא v, ולכן נוצר ההפרעה הסינוסית בתדר מרחבי, בעל מחזור של: . אם עובדים בתדר בסדר גודל של MHz, אז נקבל סריג מרווח יחסית, ונקבל זווית דיפרקציה של: .

נבחין כי כל סדר מקבל הסחת דופלר (ראה אפקט דופלר) לפי m, נקבל:
עבור תדר מרחבי יחסית נמוך, נתייחס לסריג כאל סריג דק - ולכן זו דפרקציית Raman-Nath (איור 9).
אך כאשר התדר המרחבי גבוהה (סדר גודל של MHz או GHz) אז המרחק בין ההפרעות קטן מאוד ביחס לעובי הכביש – ונקבל במקרה זה את אפקט Bragg, שבו מתקבל סדר 0 ועוד סדר נוסף שהוא דומיננטי (איור 9). באפקט Bragg מקבלים שזווית הדיפרקציה היא פעמיים את זווית הפגיעה ומתקיים:
ייצור
במקור, היה ניתן לייצר סריגים ברזולוצייה גבוהה, אך ורק על ידי מנועים מיוחדים שיצירתם הייתה מלאכה לא מבוטלת. ב־1899 עיצב הנרי יוסף גרייסון מכונה המייצרת סריגי עקיפה ברזולוציה של 120,000 קווים לאינץ'. מאוחר יותר ניתן היה לייצר סריגים תבנית התאבכות הולוגרפית. לסריגים הולוגרפיים חריצים סינוסואידליים השימושיים מאוד במונוכרומטורים. שיטה נוספת לייצור סריג עקיפה הנקרא - (volume phase holography diffraction gratings (VPH היא על ידי ג'ל הרגיש לאור, אותו ניתן להאיר בתבנית התאבכות הולוגרפית וע"י כך לאפנן באופן מחזורי את מקדם השבירה של הג'ל, וכל זאת ללא חריצים פיזיים, כך שניתן להתגבר על אפקטים לא רצויים של פיזור אור מהמשטח, הנפוצים בקרב סריגים מסוגים אחרים. לסריגים מסוג זה בדר"כ ישנה נצילות גבוהה יותר וניתן לשלב תבניות מסובכות יותר בסריג בודד.
כיום ישנו שימוש בטכנולוגיות מוליכים למחצה על מנת לאכל סריגים בעלי תבניות התאבכות הולוגרפיות בחומרים עמידים כגון סיליקון מותך. בדרך זו ניתן לשלב בין טכנולוגיות הייצור של המוליכים למחצה, הזולות והמתאימות לייצור המוני, לבין יתרונות השימוש בטכנולוגית הולוגרפיה בסריגים.
טכנולוגית ייצור חדשה נוספת היא (digital planar holography (DPH. סריגים מסוג זה מיוצרים על ידי מחשב, ולהם מספר יתרונות, בין היתר בגמישות של ניתוב האור.
מימוש סריג על ידי אופטיקה בינארית

ניתן ליצור רכיבים שמאפננים אור על ידי שימוש באופטיקה דפרקטית. גישה אחרת שקושה בשיטת היצור שהפכה לפופולרית היא – אופטיקה בינארית.
מושג זה מציין בניית אלמנטים דפרקטיים מרובה רמות פאזה תוך שימוש במסכות בינאריות בלבד. נניח שאנו מעוניינים בצבירת פאזה מסוימת, ניתן לקבוע את הסחת הפאזה על ידי סט מערכי של רמות - 2N (יש 2 בחזקת N מסכות) רמות דסקרטיות. תהליך היצור הומצאה בארצות הברית. ברגע שהיא יצאה אל הפועל היא שימוש באלמנטים אופטיים דיפרקטיביים (המשתמשים באפקט הדיפרקציה). השיטה זולה מאוד וקל לשכפל רכיבים בדרך זו. ניתן לראות את שיטת הבנייה באיור 11.
נניח אנו רוצים לבנות סריג בעלת פונקציית פאזה "שן מסור", כך שרצינו שגובה המשולש יהיה בין הערכים הם מ-0 עד .
עבור N=3 מתקבל 8 מדרגות, כפי שניתן לראות בתמונה הבאה:
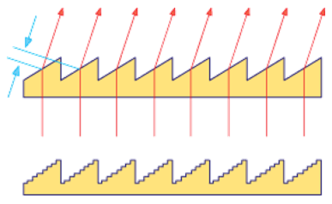
לאחר פיתוח מתמטי לפונקציית הסריג תוך שימוש באופטיקת פורייה, ניתן לקבל את הביטוי ליעילות הדיפרקציה בסדר הרלוונטי, q:
כאשר , כאשר מקדם השבירה הסביבה ו- מקדם השבירה של החומר.
נרצה שיתקבל כמה שיותר ערך שקרוב ל-, מתקבל במצב זה:
ולכן, המסקנה הנובעת היא, אם N מספר מספיק גדול אז מתקבל שעבור q ששונה מ-1, היעילות היא 0, ועבור q ששווה ל-1 היעילות היא 1. ולכן, למעשה קיבלנו שהאנרגיה נמצאת בסדר 1 כפי שציפינו במימוש שן מסור.
שימוש המסננים החוסמים
לעיתים רק אורך גל אחד רצוי ואת שאר אורכי הגל המתאימים למשוואה נרצה לחסום. נשתמש במסננים חוסמים בכניסה למונוכרומטור אשר נקבעים על ידי הספקטרום הנכנס וגלאי הרגישות.
סריגי עקיפה מרכיבים אלקטרוניים
רכיבים אלקטרוניים מסוימים מכילים דפוסים ותבניות מסוימות, כך שבפועל יש להם מאפיינים של סריג עקיפה. לדוגמה, ניתן לנתק את חיישן ה - CCD של מצלמות או פלאפונים ניידים ולהאירם במצביע לייזר וע"י תבנית ההתאבכות שנוצרת ניתן לנתח את הצורה המרחבית הפיזית של מבנה החיישן. ניתן לבצע זאת עבור רכיבים אלקטרוניים נוספים, כגון, צגי LCD ו – LED וצגי פלאפונים חכמים. מאחר שרכיבים אלו בדרך כלל מוגנים אך ורק על ידי שכבת זכוכית או פלסטיק שקופה, ניתן לבצע ניסוי זה מבלי לפגוע במכשיר עצמו. אם אין צורך בניתוח מדויק של המבנה המרחבי של הרכיב ניתן להאירו גם בפנס רגיל לקבלת תבנית התאבכות.
סריגים בחיי היום-יום ובטבע
- ישנם שימושים נפוצים בסריגי עקיפה במונוכרומטורים, ספקטרומטרים, לייזרים, מכשירים לדחיסת פולס אופטי וכלים אופטיים נוספים.


- כאשר מסתכלים על הצד האחורי של תקליטורים רואים צבעים שונים, הנוצרים מכיוון שהתקליטור הוא למעשה סריג מעגלי. תקליטורי CD ו – DVD הם דוגמאות מחיי היום יום לסריגי עקיפה, על ידי הארה עליהם ושיקוף האור על מסך ניתן להבחין באפקטים אותם הם יוצרים. יש לציין שאפקטים אלו הם תוצר לוואי הנגרר מאופן הייצור שלהם, מאחר שבתקליטורים אלו מספר רב של חריצים המסודרים בצורה מעגלית סביב מרכז התקליטור.
- חלק גדול מהצבעים של נוצות ציפורים אינם צבעים ממש, אלא נובעים מכך שהנוצות בנויות כסריגים. ריסי העיניים שלנו משמשים כסריג עקיפה גס, כך שאם כמעט נסגור את העיניים כך שמקור אור חזק מכוון לעברנו - נראה את צבעי הקשת.
- "שריר משורטט" (שרירי השלד) הוא סריג העקיפה הטבעי הנפוץ ביותר, עובדה זו עוזרת מאוד לפיזיולוגים לקבוע את המבנה של שריר מסוג זה. בנוסף ניתן לאפיין גם את המבנה הכימי של קריסטלים כסריג עקיפה, עבור סוגים של קרינה אלקטרומגנטית שאיננה בספקטרום האור הנראה, ובכך להניח בסיס לטכניקות X-ray, קריסטלוגרפיה.
- במטאורולוגיה מופיעים לעיתים אפקטים של סריג עקיפה. “diffraction coronas” הן הילות צבעוניות בצורת טבעת המופיעות סביב מקור אור, כמו השמש. תופעה זו נוסעת מאינטראקציה של האור עם חלקיקים כגון טיפות מים, קריסטלי קרח, או חלקיקי עשן הנמצאים בשמיים. כאשר החלקיקים בקירוב באותו הגודל הם שוברים את האור בזווית מסוימת (הזווית תלויה בין היתר בגודל החלקיקים). תופעה זו מתרחשת גם במקורות אור אחרים, כגון נר או פנס רחוב האפופים בערפל.

- תופעה נוספת - “cloud iridescence” בה העננים זוהרים ונוצצים בשלל צבעי הקשת ביחד עם היווצרות הילות בצורת טבעת, גם כן מתרחשת כתוצאה מדיפרקציית אור.
- עדשת פרנל.
- מאפנן אקוסטו-אופטי.
- SEED – Self Electro-optic Effect Device – מימוש שערים לוגיים.
- MQW - Multiple Quantum Well.
- Raman-Nath diffraction.
- Bragg diffraction.
- מדפסות לייזר.
קישורים חיצוניים
| פוטוניקה | ||
|---|---|---|
| תחומים | ביו-פוטוניקה • ננו-פוטוניקה • מיקרו-פוטוניקה • מחשוב פוטוני | |
| כלים | ביו פוטון • ODPSK • אינרפרומטר השהייה • EDWA • לייזר • מרבב אופטי • הייבריד אופטי • מעגל משולב פוטוני • גביש פוטוני • סיב גביש פוטוני • מוליך גל חריץ • SDOF • סופר מנסרה • TS-ADC • העברת אנרגיה אלחוטית | |
| עקרונות | מערך מוליכי גל • סריג עקיפה • סריג הולוגרפי • שיטת מונטה קרלו • מיתוג ארכי גל • קוהרנטיות אטומית • מיקרוגל פוטוניקה • שיבוט אוטומטי • מצב חשוך • דיפוסיה פוטונית | |
| יישומים | רשת ניורונית אופטית • מפרש שמש • תקשורת אופטית | |
| ראו גם | אופטיקה • אלקטרואופטיקה | |
סריג עקיפה32833258Q653294





































































