משולש פנרוז

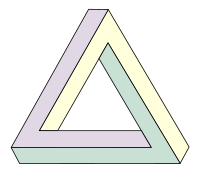
משולש פנרוז עם קורות מקוטעות

משולש פנרוז הוא עצם שלא יכול להתקיים במציאות שהגה ב-1934 האמן השוודי אוסקר רטרסוורד (Oscar Reutersvärd). גם המתמטיקאי רוג'ר פנרוז ניסח את האפיון שלו באופן עצמאי, ופרסם אותו בשנות ה-50 של המאה ה-20, כשהוא מתאר אותו כ"בלתי אפשרי בצורתו הטהורה ביותר".

משולש פנרוז מורכב משלוש קורות ריבועיות ישרות (תיבות ריבועיות), היוצרות יחדיו משולש כך שהזווית בין כל שתי קורות היא זווית ישרה. לפעמים מציירים את המשולש כך שהקורות מקוטעות ומחולקות לקוביות.

מאפייני המשולש

משולש פנרוז אינו קיים במרחב אוקלידי התלת-ממדי. עם זאת ישנן יריעות תלת-ממדיות מופשטות בהן המשולש קיים.

אשליית קיומו של המשולש נוצרת מכיוון שהמוח האנושי מפרש את התמונה הדו-ממדית כהיטל של גוף תלת-ממדי. כל חלק במשולש פנרוז בנפרד, נדמה כייצוג לגיטימי של אובייקט תלת-ממדי (למשל, אין בעיה בכך ששתי קורות אכן ייפגשו בזווית ישרה). עם זאת, צירוף כל החלקים יחדיו לא ייתכן מוחשית.

ניתן ליצור אשליה אופטית תלת-ממדית של משולש פנרוז, על ידי בניית הקורות כך שמזוויות מסוימות ייראה כאילו הן מתחברות ליצירת המשולש, בעוד שבפועל הן אינן נפגשות בקודקוד אחד. אפשרות אחרת היא לבנות את הקורות כך שנדמה כי הן ישרות, בעוד שבפועל הן עקמומיות.

משולש פנרוז בתרבות

משולש פנרוז בולט ביצירותיו של מאוריץ קורנליס אשר. יצירותיו המוקדמות העוסקות בעצמים שקיומם הפיזי לא אפשרי ובהסתכלות מפרספקטיבה ייחודית. כך עשה למשל בציור "הגשר" (1930). עיסוקו זה בבלתי אפשרי, היווה את חלק מההשראה להגיית הרעיון של משולש פנרוז.

המשולש מופיע בליתוגרפיה "מפל המים" של אשר (1961), המתארת אפיק מים הזורם בצורת זיגזג, לאורך הדפנות של שני משולשי פנרוז מאורכים, כך שהם מסתיימים בגובה של שתי קומות מעל לגובה בו החלו, ובתוך כך נוצר מפל המניע גלגל מים.

במספר מקומות בעולם קיימים פסלים המתארים כביכול משולשי פנרוז: במזרח פרת' שבאוסטרליה; במוזיאון הגרמני לטכנולוגיה בברלין; בקרינתיה שבאוסטריה; בפארק המדע של גְרָנָדָה שבספרד; באופובן (Ophoven) שבבלגיה, ואף בגן המדע שנמצא במכון ויצמן שברחובות.

פסל "משולש בלתי אפשרי" במזרח העיר פרת' באוסטרליה. מזוויות מסוימות נראה שהקורות נפגשות בקודקוד העליון, אף על פי שאין זה כך, וכך נוצרת אשליית משולש פנרוז.