מספר מצולע

במתמטיקה, מספר מצולע, הוא מספר של עצמים, כגון חלוקי נחל, שאפשר לארגן כקודקודים של שרשרת מצולעים משוכללים בעלי קודקוד משותף. מקורם בחשיבה הפיתגוראית על מספרים, שלפיה יש לייצג אותם באמצעות עצמים מוחשיים. הדוגמאות הפשוטות ביותר הן מספרים משולשיים, שהם מספרים מהצורה $\ {\frac {n(n+1)}{2}}$, ומספרים ריבועיים, מהצורה $\ n^{2}$. באופן כללי, מספרים שאפשר לסדר כקודקודים של שרשרת מצולעים בעלי k צלעות הם מהצורה: $\ n+(k-2)T_{n-1}=n+(k-2){\frac {n(n-1)}{2}}$, כאשר $T_{n-1}$ הוא המספר המשולשי ה-n-1. נוסחה זו מוצדקת על ידי חלוקת המצולע למשולשים.

מתמטיקאים במאות ה-17 וה-18 עסקו במספרים מצולעים. פרמה שער את משפט המספרים המצולעים. ב- 1730 מצא אוילר את הנוסחה הכללית למספרים שהם גם משולשים וגם ריבועיים, באמצעות פתרון של משוואת פל מתאימה.

דוגמאות וציורים

לדוגמה, המספר 10 הוא מספר משולשי, משום שאפשר לארגן אותו בצורת משולש משוכלל:

את המספר 10 לא ניתן לתאר בצורת ריבוע; את 9 אפשר (ראו מספר ריבועי):

ישנם מספרים שאפשר לארגן גם בצורת משולש וגם בצורת ריבוע, למשל 36 (ראו מספר משולשי ריבועי):

השיטה להגדלת מצולע לגודל הבא הוא להוסיף לשתי צלעות סמוכות נקודה אחת ואז להוסיף את כל הנקודות הדרושות לצדדים בין שתי הנקודות האלה. בדיאגרמה להלן, כל שכבה נוספת מוצגת בצבע אדום.

מספרים משולשים

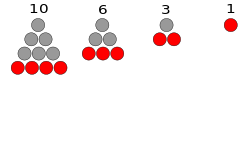
בין היתר ניתן למצוא את המספרים המשולשים בתור העמודה השנייה של משולש פסקל.

מספרים ריבועיים

מצולעים עם מספר גדול יותר של צלעות, כמו מחומשים ומשושים, יכולים להיות מיוצגים גם כן בנקודות (עם המוסכמה ש-1 הוא מספר מצולע לכל מספר של צלעות).

מספרים מחומשים

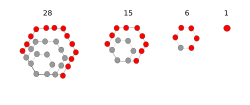
מספרים משושים

שם	נוסחה	n=1	2	3	4	5	6	7	8	9	10	11	12	13
משולש	½n(1n + 1)	1	3	6	10	15	21	28	36	45	55	66	78	91
ריבוע	½n(2n - 0)	1	4	9	16	25	36	49	64	81	100	121	144	169
מחומש	½n(3n - 1)	1	5	12	22	35	51	70	92	117	145	176	210	247
משושה	½n(4n - 2)	1	6	15	28	45	66	91	120	153	190	231	276	325
משובע	½n(5n - 3)	1	7	18	34	55	81	112	148	189	235	286	342	403
מתומן	½n(6n - 4)	1	8	21	40	65	96	133	176	225	280	341	408	481
x-צלעות	((n((x-2)n-(x-4½	1	x	3x-3	6x-8	10x-15

לקריאה נוספת

• The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books), 1997
• Figurate Numbers, 2011 [1]

קישורים חיצוניים

• מספר מצולע, באתר MathWorld (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32665309מספר מצולע