מחשב הפסיעות

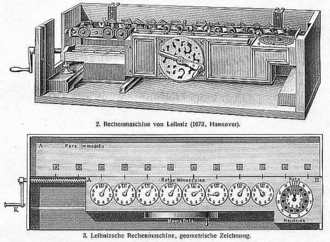
מחשב הפסיעות של לייבניץ בתצוגה במוזיאון הגרמני.

מחשב הפסיעות (באנגלית: Stepped Reckoner) היה מכונת חישוב מכנית, שהומצא על ידי המתמטיקאי הגרמני גוטפריד וילהלם לייבניץ בסביבות 1672, ושבנייתו הושלמה ב-1694. זה היה המחשב המכני הראשון שיכול היה לבצע את כל ארבע הפעולות האריתמטיות.

על אף ההיתכנות התאורטית ואבות הטיפוס שיוצרו למחשב הפסיעות, הרי מבנה גלגלי השיניים המורכב שבבסיסו היה מעבר לטכנולוגיות הייצור של התקופה; בעיות תכנוניות, כמו גם פגם תכנוני של מנגנון הנשא שלו (carry mechanism) מנעו מהמכונה תפקוד אמין.

על אף הפגמים המכניים של מחשב הפסיעות, הוא הדגים את ההיתכנות של מכונות חישוב עתידיות. ברכיב הבסיסי של המכונה, שהומצא על ידי לייבניץ, שנקרא התוף המדורג, נעשה שימוש במכונות חישוב מתקדמות יותר במשך 200 השנים הבאות, ואף עד לשנות ה-70 של המאה ה-20, דרך מחשבון הקורטה הידני.

תיאור

תרשים של מחשב הפסיעות משנת 1897. התרשים מציג גרסה שיכולה לצבור מספרים עד ל-12 ספרות.

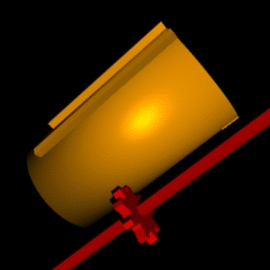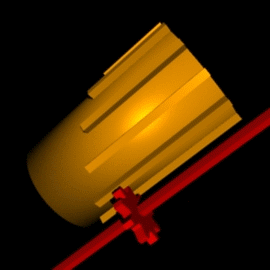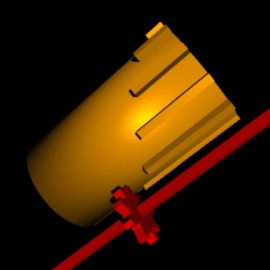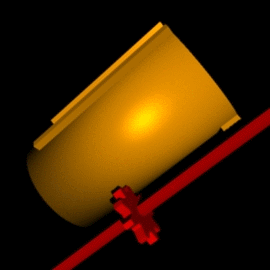
מחשב הפסיעות התבסס על מנגנון גלגלי שיניים שלייבניץ המציא מוקדם יותר שנקרא התוף המדורג (stepped drum) או גם גלגל לייבניץ. התוף המדורג הינו גליל שלאורך היקפו בליטות באורכים שונים - שיניים, המסודרות כך שאורכיהן מהווים סדרה חשבונית. באמצעות הזחה של גלגל השיניים, הנמצא במגע עם שיני התוף המדורגות, לאורך צירו, מושגת שליטה על מספר הסיבובים שגלגל השיניים יסוב, כמומחש באנימציה מימין, ויסובב את משנהו.

גלגל לייבניץ. ניתן לראות כי שלוש מתוך השיניים של התוף המדורג נוגעות בשיני גלגל השיניים ולכן הוא ייסוב שלוש פעמים

לא ברור כמה אבות טיפוס של המכונה נבנו. התרשימים משמאל מראים גרסה שיכולה לצבור מספרים בני 12 ספרות. החלק הזה^{[דרושה הבהרה]} מתאר את אב הטיפוס בן 16 הספרות ששרד בהנובר.

מכונת החישוב היא באורך של 67 סנטימטר ועשויה מפליז ופלדה מלוטשת. היא מורכבת משני חלקים צמודים מקבילים; אקומולטור בחלק האחורי של המכונה, שיכול להציג עד 16 ספרות עשרוניות, ומנגנון הזנת הקלט שבחזית, אליו ניתן להזין מספרים בני 8 ספרות עשרוניות. בחלק הקלט ישנן 8 חוגות עם כפתורים המאפשרות להזין את האופרנד, כמו גם חוגה דמוית חוגת-טלפון כדי להזין את ספרת המולטיפליקנד, וכננת בחזית שבעזרתה מבצעים את החישוב. תוצאת הפעולה המתמטית מופיעה על 16 החלונות בחלק האקומולטור האחורי. החלק אליו מזינים את הקלט מוצב על מסילה כך שניתן להניע אותו במקביל לאקומולטור בעזרת ידית שבצידי המכונה שמסובבת מעיין בורג שמניע את מנגנון הזנת הקלט, וכך ניתן לבצע גם תהליכי כפל של מספרים דו ספרתיים ויותר.

מחשב הפסיעות יכול:

• להוסיף או לחסר מספר בן 8 ספרות ממספר בן 16 ספרות.
• להכפיל שני מספרים בני 8 ספרות כדי לקבל תוצאה בת 16 ספרות.
• לחלק מספר בן 16 ספרות במחלק בן 8 ספרות.

הוספה או החסרה מבוצעת בצעד יחיד, באמצעות סיבוב של הידית. כפל וחילוק מבוצעים ספרה ספרה על ספרות המולטיפליקנד או המחלק, בפרוצדורה שמקבילה לתהליכים של כפל ארוך וחילוק ארוך הנלמדים בבית ספר. אפשרית גם סדרת פעולות על התוצאה שבאקומולטור: למשל ניתן לחשב שורשים של מספרים באמצעות סדרה של פעולות חילוק וחיבור.

המבנה הפנימי של המכונה

שרטוטו של לייבניץ המראה כיצד יש להכפיל את 365 ב-124.

המכניזם של המכונה ניתן לחלוקה לשני חלקים. החלק שמציג את הפלט (על ידי 16 חלונות) אינו נייד ונקרא על ידי לייבניץ Pars immobilis. החלק בו מזינים את האופרנד הינו נייד ונקרא על ידי לייבניץ Pars mobilis.

מנגנון הזנת האופרנד

כפי שהוסבר מקודם, האופרנד המוזן הוא 8-ספרתי; בחלק הנייד ישנן 8 חוגות אשר ניתן לסובב כל אחת מהן כך שתייצג את הספרה המתאימה של האופרנד. מאחורי כל חוגה בחלק זה נמצא תוף מדורג יחיד S, אשר הינו מצומד לפס שיניים M (איור מופיע במקור שהובא למטה), שזה בתורו מצומד לגלגל שיניים E. החוגה וגלגל השיניים E הן בעלות ציר משותף. באמצעות סיבוב החוגה ניתן לשנות את מצבו של התוף המדורג; על ידי סיבוב החוגה עד לספרה מתאימה, גלגל השיניים E מסתובב גזרה זוויתית מסוימת, והצימוד עם פס השיניים יוצר המרה של תנועת הסיבוב של הגלגל E לתנועה קווית של פס השיניים ושל ציר התוף המדורג. התוף המדורג נושק לגלגל שיניים נוסף F אשר הוא בעל ציר משותף עם חוגת הפלט - כלומר הזנת הקלט ה-8 ספרתי מציבה את 8 התופים המדורגים בפוזיציות שונות, וכך מאפשרת להם להעביר שבר מדוד של סיבוב שלם לגלגלי השיניים של תצוגת הפלט (בכל סיבוב שלם של התופים המדורגים).

מנגנון הזנת המולטיפליקנד

לאחר שהוזן הקלט ה-8-ספרתי, נותר להזין את המספר בו רוצים להכפיל. הזנת המספר בו מכפילים מתבצעת ספרה ספרה, בדומה לכפל ארוך. אם ברצוננו להכפיל במספר בן ספרה אחת, כל שיש לעשות הוא לסובב את הגלגל הגדול, הנקרא Magna rota, מספר סיבובים הזהה לספרה בה רוצים להכפיל. כל סיבוב של גלגל זה גורם לתופים המדורגים להשלים סיבוב אחד סביב צירם. הפלט שיופיע בתצוגה של 16 החלונות ייצג את תוצאת ההכפלה. לנוחיות התפעול, בצידה של המכונה ישנו מונה של מספר הסיבובים של גלגל ה-Magna rota עד כה (שנקרא Rota magnuscula), כך שהמפעיל לא יאלץ לזכור כמה סיבובים ביצע. אם ברצוננו לכפול את הקלט במספר רב-ספרתי, אז יש לכפול בספרת היחידות, ולאחר מכן יש לסובב את הידית הצדדית (המחוברת לגלגל הבורגי) כך שהחלק הנייד כולו יזוז ספרה אחת, ורק לאחר מכן לכפול בספרת העשרות, וכך הלאה עבור ספרת המאות וספרות גבוהות יותר. מנגנון ההוספה של המכונה מחבר את כל תוצאות ההכפלות בכל ספרה לכדי תוצאה אחת המוצגת בחלונות הפלט.

פעולות מתמטיות אחרות

הדגמת ביצוע תהליך ההכפלה מתמצתת במידה מסוימת את יכולות המכונה. עם זאת יש לציין גם כיצד מתבצעות פעולות מתמטיות אחרות. חיבור הינו הפעולה הפשוטה ביותר לביצוע, ומתבצע באמצעות צעד חישובי יחיד. כדי לחבר שני מספרים, יש להזין מחובר אחד לחלונות הפלט (המכונה מכילה מנגנון לסיבוב גלגלי הפלט, כמו גם מנגנון לאיפוס התוצאה), לאחר מכן להזין את המחובר השני לחלונות הקלט, ולבסוף לסובב את גלגל ה-Magna rota פעם אחת (כלומר הוספת המחובר השני היא כמו הוספת כפולה שלו ב-1). מנגנון ההוספה המובנה של המכונה מחבר את שני המספרים באופן אוטומטי, והמספר המתקבל בתצוגת הפלט הוא הסכום. חיסור מתבצע באופן דומה, אלא שיש לסובב את גלגל ה-Magna rota בכיוון ההפוך; בדרך זו התופים המדורגים מסתובבים במגמה הפוכה כך שמתקבל למעשה חיסור של מחסר ממחוסר. כדי לבצע חילוק ארוך של מספר X במספר Y, יש להוסיף מספר מרבי של אפסים מימין למספר Y כך שעדיין Y בתוספת האפסים יהיה קטן מ-X (נניח שהוספנו n אפסים), להזין את Y בתוספת האפסים כקלט, ולאחר מכן לסובב את גלגל ה-Magna rota מספר פעמים m עד אשר המספר בתצוגה האחורית (תצוגת הפלט) יהיה קטן מהמחלק (Y בתוספת האפסים). קריאת הספרה הראשונה (השמאלית ביותר) אינה מתבצעת דרך תצוגת הפלט אלא דרך קריאת מונה הסיבובים בצידה של התצוגה (ה-Rota magnuscula), והספרה m שמופיעה בו היא הראשונה והשמאלית ביותר במספר בן 1 + n ספרות. לאחר מכן יש לחזור על התהליך, אלא שהפעם המחלק יהיה המספר Y בתוספת n - 1 אפסים, וכך הלאה. קריאת מונה הסיבובים בכל שלב בתהליך מייצגת את הספרה המתקבלת החדשה של המספר, באופן אנלוגי לתהליך החילוק הארוך.

היסטוריה

מנגנון מחשב הפסיעות

לייבניץ הגה את הרעיון של מכונת החישוב שלו ב-1672 בפריז, לאחר שבחן את עקרונות הפעולה של פדומטר שנתקל בו. מאוחר יותר הוא התוודע למכונת החישוב של בלז פסקל (הפסקלין) כאשר הוא קרא את "הגיגים" של פסקל. הוא התרכז בהרחבת ישימותו של המכניזם של פסקל כך שיוכל גם להכפיל ולחלק. הוא הציג מודל מעץ של מכונת החישוב החדשה שלו בפני החברה המלכותית בלונדון ב-1 בפברואר 1673 וזכה להערכה ולעידוד רב. במכתב מ-26 במרץ 1673 ליוהאן פרידריך, שבו הוא הזכיר את הפרזנטציה שערך בלונדון, לייבניץ תיאר את התכלית של "המכונה האריתמטית" כביצוע חישובים "בקלות, במהירות, ובאופן מדויק". לייבניץ הוסיף גם שבאופן תאורטי המספרים המחושבים יכולים להיות גדולים ככל האפשר, אם רק מתאימים את הגודל של המכונה – הוא צוטט כאומר: "מספר יכול להכיל סדרה של ספרות, ארוכה ככל שנרצה (בפרופורציה לגודל של המכונה)".

הוא בנה את המכונה המוקדמת שלו העשויה מפליז בין השנים 1674 ו-1685. המכונה שלו שבנה בשנותיו המאוחרות יותר נבנתה בין השנים 1686 ו-1694.

מקורות

• מאמר מעולה על מחשב הפסיעות הוא המאמר הבא: The Stepped Reckoner of Gottfried Leibniz

קישורים חיצוניים

מדיה וקבצים בנושא מחשב הפסיעות בוויקישיתוף