מחסום ארליך-שוובל

מחסום אֶרְלִיךְ-שְווֵבֶּל (באנגלית: Ehrlich-Schwöbel Barrier), או ESB, הוא מחסום אנרגטי לדיפוזיה של אטומים על פני השטח של גביש, שעליו עליהם להתגבר כדי לחצות שפת מדרגה (איור 1). כאשר קיים מחסום כזה בשפת המדרגה יתקשו האטומים המפעפעים על פי השטח, האדאטומים (אנ'), לעבור את שפת המדרגה ולרדת למישור האטומי הנמוך יותר. לאדאטומים אלו תהיה, לכן, הסתברות גבוהה יותר להיות מוחזרים חזרה למדרגה (לטרסה) ממנה באו. מחסום נוסף זה התגלה על ידי גרט ארליך (גר') ו-F. G. Hudda, ממעבדות המחקר של ג'נרל אלקטריק (אנ') בסקנקטדי (ניו יורק) ב-1966, במהלך צפייה בשיקוע טיטניום על טיטניום במיקרוסקופ שדה יוני (אנ').[1] מיד אחר כך תיארו אותו תאורטית ריצ'רד שוובל, מהמעבדות הלאומיות סַנְדִייָה (אנ') באלבקרקי (ניו מקסיקו), ואדוארד ג'יי שיפסי (Shipsey), מאוניברסיטת המדינה של אוהיו בקולומבוס.[2][3] הם גם ציינו שלמחסום זה יש השפעה מייצבת על הגידול של גבישים באופן של זרימת מדרגות.
סיבת המחסום
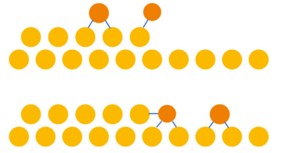
איור 2 מסביר מניין נובע מחסום ארליך-שוובל: האדאטום מהמדרגה (הטרסה) העליונה צריך לשבור קשרים כימיים עם האטומים שעל פני המדרגה, בניסיונו לעבור את השפה היורדת של המדרגה, כדי להיכנס לאתר התגבשות. מהטרסה התחתונה, לעומת זאת, האדאטום יוצר קשרים נוספים עם האטומים שבמדרגה, והאנרגיה שלו קְטֵנָה. לקונפיגורציה של הקשרים הבודדים על פני השטח יש השפעה על הקישור של האדאטומים מעל ומתחת לשפת המדרגה. לפיכך גובה המחסום תלוי בחומר, בכיוון הגבישי של פני השטח וברקונסטרוקציה המשטחית (אנ') (התלויה, מצידה, בטמפרטורה ובשטף האטומים המגיע לפני השטח).
השפעת המחסום על גידול גבישים ואפיטקסיה
מחסום האנרגיה הנוסף בשפת המדרגה מקטין את קבוע ההצטרפות של אדאטומים לשפה מהמדרגה העליונה, יחסית לזה מהמדרגה התחתונה. מידת הא-סימטריה בקצבי ההצטרפות תלויה בגובה המחסום, אך גם בתנאי הגיבוש. בטמפרטורות גידול גבוהות מספיק, לאדאטומים תהיה אנרגיה מספקת לדלג בקלות מעל למחסום זה. יש, אם כן, להתחשב בשני גורמים: מחסום ארליך-שוובל עצמו (מידת ההבדל בהסתברויות הלכידה של אדאטומים מהמדרגה העליונה ומהמדרגה התחתונה) ותנאי הגידול.
ל-ESB השפעה על התפתחות המדרגות במהלך גידול גבישים ובאפיטקסיה. ההשפעה יכולה להיות מייצבת, זאת אומרת שהפרעה על פני השטח (למשל רוחב מדרגות שונה) תדעך עם התקדמות הגידול (פני השטח מתפתחים כך שלכל המדרגות רוחב דומה). אך מחסום זה יכול לגרום גם לתופעות של חוסר יציבות בגידול (יצירת תלוליות על פני השטח, מדרגות מתפתלות, וקיבוץ מדרגות). ה-ESB משפיע גם על הטמפרטורה הקריטית למעבר מזרימת מדרגות (Step Flow – SF) לגרעון איים דו-ממדיים (two dimensional island growth – 2D-IG).
הטמפרטורה הקריטית למעבר מ-SF ל-2D-IG
במהלך רישום אוסצילציות RHEED במהלך הומו-אפיטקסיה של GaAs באפיטקסיית קרן מולקולרית (MBE) על מצעים ויסנליים (שפני השטח שלהם במיסאורינטציה קלה ממישור גבישי ראשי, ולכן יש עליהם מערך מדרגות) כפונקציה של טמפרטורת הגידול, הבחינו ניב (Neave) וחבריו בהעלמות האסוצליציות כשטמפרטורת הגידול ירדה מתחת לטמפרטורה מסוימת.[4] בטמפרטורות נמוכות מטמפרטורה קריטית זו יש לאדאטומים ניידות נמוכה (כלומר מרחק דיפוזיה קצר), כך שלפני שהם מצליחים להגיע לשפת המדרגה התוחמת את הטרסה, הם פוגשים האחד את השני, ומתגרענים לגרעין גיבוש דו-ממדי. גרעון דו-ממדי זה על הטרסות מניב את האוסצילציות בעוצמת ה-RHEED. בטמפרטורות גבוהות, לעומת זאת, אין גרעון כזה, כי לכל האדאטומים יש ניידות מספקת (מרחק דיפוזיה ארוך מספיק) כדי להגיע אל שפות המדרגות ולהילכד בהן – אופן גידול של זרימת מדרגות.

את סוג הגידול, איים דו-ממדיים והתמזגותם (2D-IG, פנל (a) באיור 3) או זרימת מדרגות (SF, פנל (b) באיור 3), קובע, אם כן, היחס בין מרחק הדיפוזיה של האדאטומים ובין הרוחב הממוצע של המדרגות. כשיחס זה נמוך (טמפרטורת גידול נמוכה או מדרגות רחבות, כלומר זווית מיסאורינטציה קטנה של פני השטח ביחס למישור גבישי ראשי) הגידול יתקדם במנגנון 2D-IG; וכשליחס הזה ערך גדול (טמפרטורה גבוהה או מדרגות צרות וצפופות - זווית מיסאורינטציה גבוהה) תתקבל זרימת מדרגות.
נניח לרגע שבשפת המדרגות בפני השטח יש מחסומי ES גבוהים אינסופית (∞ = ESB, פנל (c) באיור 3). במקרה זה אף אדאטום לא יכול לעזוב את המדרגה על ידי ירידה מטה. אם האדאטומים אינם מתנדפים (אין דסורפציה) אז עליהם לפעפע את כל רוחב המדרגה עד לשפה העולה ולהצטרף אליה (או לחזור חזרה למדרגה עליה היו). לכן, מרחק הדיפוזיה הנדרש לכל האטומים על המדרגה על מנת להגיע לשפת המדרגה הַגְּדֵלָה הוא רוחב המדרגה עצמה. בקיצון השני, כאשר אין מחסום כלל (ESB = 0, פנל (d) באיור 3), מרחק הדיפוזיה הדרוש הוא רק חצי רוחב המדרגה. (ועבור מחסום בגובה סופי, מרחק הדיפוזיה נמצא בין שני ערכי הקיצון האלה.) כלומר, בנוכחות מחסום ES, המעבר מזרימת מדרגות (גרעון חד-ממדי) לגידול איים דו-ממדיים מתרחש כאשר היחס מרחק דיפוזיה לרוחב מדרגה גדול יותר מאשר בהיעדר המחסום בשפת המדרגה. מצב זה מוראה סכמטית בפנל המרכזי שבאיור 3. למשל, ברוחב מדרגה מסוים הנתון על ידי הקו האופקי 'AA באיור 3 רק מתחת למרחק דיפוזיה שערכו C יתקבל 2D-IG אם ESB = 0, ואילו אם ∞ = ESB המעבר מ-2D-IG ל-SF יקרה רק כאשר מרחק הדיפוזיה גדול מ-D. אם המדרגות על פני השטח רחבות יותר ('BB באיור 3), המעברים הללו יתרחשו במרחקי דיפוזיה גדולים יותר: E ו-F, בהתאמה. הטמפרטורה הקריטית למעבר מ-2D-IG ל-SF תשתנה, אם כן, על פי הקווים האלכסוניים עם ESB = 0 ועם ∞ = ESB כמוראה בפנל המרכזי שבאיור 3.
ההשפעת המייצבת של ESB בגידול בזרימת מדרגות על מצעים ויסינליים - החלקת פני השטח

למחסום ES יכולה להיות השפעה מטיבה על הגידול אם הוא מתקדם באופן זרימת מדרגות (SF), שכן המשמעות של מחסום זה היא שלאדאטומים יש סיכוי גבוה יותר להצטרף לשפת המדרגה העולה (כלומר מהטרסה שמלמטה) מאשר ליורדת (מהטרסה שמעליה – איור 4). זאת אומרת, שהאדאטומים (העיגולים הכהים באיור 4) שמצטרפים לכל שפת מדרגה מגיעים בעיקר מהטרסה שמתחתיה, זו שלפני השפה העולה. בפני שטח כאלו, עם מדרגות במרווחים לא אחידים, מגיע אל שפת מדרגה שלפניה טרסה צרה שטף אדאטומים נמוך (מצוין בחץ כחול דק באיור 4), כי שטח האיסוף שלה קטן, ולכן היא מתקדמת לאט. לעומת זאת לשפת מדרגה שלפניה טרסה רחבה, כלומר שיש לה שטח איסוף גדול, מגיע שטף גדול של אדאטומים (חץ כחול עבה), והיא מתקדמת מהר יותר. כך שההפרעה דועכת עם התפתחות הגידול: המדרגות נהיות בעלות רוחב דומה. אפקט חשוב זה משמש באפיטקסיה להחלקת פני השטח של המצע על ידי גידול שכבה חוצצת (באפר) הומו-אפיטקסיאלית או הטרו-אפיטקסיאלית עם קוואזי תאום סריגי.
ההשפעה המערערת של ESB בגידול על מצעים סינגולריים - גידול תלוליות

על פני שטח סינגולריים (מישור גבישי ראשי כלומר בעל אינדקס מילר נמוך) או בפני שטח ויסינליים עם זווית מיסאורינטציה נמוכה כלפי מישור סינגולרי (כאשר המדרגות רחבות) מחסומי ארליך-שוובל מובילים ליצירה של מבנים בצורת פירמידות (תלוליות) על פני השטח, כמוראה באיור 5. מצב זה תואר לראשונה בשנת 1991.[5] מפני שלאדאטומים אין שפת מדרגה להצטרף אליה הם מצטברים על פני השטח החלקים, ומתישהו יוצרים גרעין גיבוש חד-שכבתי. כך נוצרות שפות, שאליהן מצטרפים אדאטומים מהטרסה התחתונה, המקורית, ומגדילים אותו לאי דו-ממדי (t1 באיור 5). בגלל מחסום ES האדאטומים מוחדרים לשריג הגדל בשפות של האי הזה. יש לכך שתי תוצאות: ראשית, האי מתרחב לטרלית עד אשר אירוע גרעון דו-ממדי נוסף יכול להתרחש עליו (t2 באיור). משזה קורה האי החדש מתרחב לטרלית עד אשר מתגרען עליו אי נוסף (t3), וכך ממשיך התהליך הלאה, תוך יצירת תלולית. שנית, מאחר שאין (כמעט) דיפוזיה כלפי מטה, רק האדאטומים שמגיעים מהשטח שבין האיים הדו-ממדיים הללו יכולים להזין את שפת המדרגה הנמוכה ביותר, ורק האדאטומים המצויים על שפת המדרגה הנמוכה ביותר יכולים להזין את השפה של המדרגה השנייה מלמטה. אם כן, מאחר שאדאטומים מוחזרים מהשפות של מדרגות יורדות ומצטרפים באופן מועדף לשפות של מדרגות עולות, הזרם הוא כלפי מעלה – "במעלה ההר".[6] זרם תְּלוּי גידול זה של האדאטומים על פני השטח הוא המקור לאי-יציבות, שגורמת לתלוליות. הריכוז של האדאטומים המפעפעים על פני השטח נשמר על ידי שטף האטומים הפוגע, ועל כן הזרם על פני השטח הוא אפקט של אי-שיווי משקל.
מורפולוגיות טיפוסיות הנוצרות על ידי מחסום ES הן תלוליות עם טרסות מוגדרות היטב, כך שהן נראות כמו עוגות חתונה,[6] או פירמידות מקסיקניות (התלולית השמאלית שבאיור 6). הצורה המדויקת של תלוליות אלו נקבעת על ידי גובהו של מחסום ES. עבור מחסומים נמוכים, הן גדולות ושטוחות עם סדקים עמוקים ביניהן, בעוד שעבור מחסומים גבוהים התלוליות גבוהות ובעלות ממד לטרלי קטן. עם התקדמות הגידול מתמזגות התלוליות לכדי שכבה רציפה, כשהמדרגות החיצוניות של האיים נפגשות. עם זאת מאחר שהדיפוזיה מטה מוגבלת, ייתכן שייווצרו פגמים בגבולות אלו. יתרה מכך, יש אפשרות שהדיפוזיה מטה משתנה כאשר שפת המדרגה מגיע לפאה (פסטה) בכיוון גבישי מסוים. פאה כזו יכולה לייצב את האינקורפורציה, או אף לגרום לאינקורפורציה שונה, של זיהומים.
ראוי להבדיל בין התלוליות בצורת "עוגת חתונה" הנוצרות בגלל ESB בשפות המדרגות (כמו התלולית השמאלית באיור 6) ובין פירמידות ספירליות (התלולית הימנית באיור 6) שהן תוצאה של גידול סביב נקע בורגי (או הרכיב הבורגי של נקע) שמצוי בפני המצע, כפי שהסביר פרנק.[7] הנקע הבורגי מספק לאדאטומים את אתרי ההצטרפות לגביש, בהיעדר שפות מדרגה על פני השטח הסינגוליים.
ההשפעה המערערת של ESB על שפות המדרגות - התפתלות מדרגות

כמו שרק לעיתים רחוקות פני שטח הם חלקים לגמרי, כך גם רק לעיתים רחוקות תהיינה מדרגות אמתיות ישרות לגמרי. המדרגות משוטטות אנה ואנה בסקלת מרחק קצרה מאד. הדבר נכון בעיקר במהלך הגידול כאשר המדרגה אוספת אליה אדאטומים חדשים. אפילו אם המדרגה הייתה ישרה לגמרי בהתחלה, צורתה חייבת להשתנות כדי שהגידול יתרחש. כך שעל פני שטח ויסינליים עם זוויות מיסאוריינטציה נמוכות, ההשפעה המערערת של מחסום ארליך-שוובל מתבטאת לא רק בהופעת תלוליות, אלא גם בהופעת מורפולוגיה של התפתלות מדרגות (step-meandering).
התיאור הסכמטי באיור 7 מדגים זאת: על פני שטח הגביש ישנן בזמן t=0, במקרה זה, שתי מדרגות, כשהימנית מהשתיים מפותלת יותר מהשמאלית. קיומו של מחסום ארליך-שוובל בשפות המדרגות גורם לכך שהאדאטומים המטיילים על המדרגה הנמוכה הם שיקבעו את קצב התקדמות המדרגה. לאדאטומים אלו קל יותר להגיע לבליטה (החץ הכחול) מאשר ל"שקע" (החץ האדום). לכן הבליטה תגדל מהר יותר, ושפת המדרגה תתעוות יותר ויותר. כתוצאה מהגידול מתקדמות שתי המדרגות ימינה (הפנל הימני בזמן t1; מקום השפות בתחילת הגידול, ב-t=0, מצוין בפנל זה על ידי הקווים המרוסקים). המדרגה הימנית יותר, המפותלת, נעה מרחק רב יותר (כי שטח האיסוף שלה גדול יותר) ונהייתה מפותלת יותר.

עד כה התייחסנו ל-ESB בשפת המדרגה היורדת – אפקט דו-ממדי הקרוי לעיתים SESE (step Ehrlich‑Scwöbel effect). יש גם אפשרות ל-ESB חד-ממדי במעבר האדאטומים על פני ברך (kink) בזמן שהם נעים לאורך שפת המדרגה: KESE (kink Ehrlich-Scwöbel effect). מצב זה מתואר באיור 8. קיום המחסומים בנקודות הברך יגרום לתופעות דומות לאלו של SESE אך בחד-ממד. שתי נקודות ברך סמוכות עם כיוונים הפוכים בזמן t=0 תגרומנה להתפתחות תלולית חד-ממדית, שבהתפתחותה (זמנים t1 ו-t2) תיצור מעין "אצבע" – התפתלות של המדרגה. זהו מצב דומה למתואר באיור 5 אלא שהפעם נקודת המבט היא כלפי פני השטח מלמעלה, כשהעיגולים הבהירים מייצגים את שטח המדרגה, והעיגולים הכהים מייצגים את האדאטומים הנעים על גבי השפה. התפתלות המדרגה כתוצאה מ-ESB חד-ממדי נקראת גם האי-יציבות של ביילס-זנגוויל (Bales-Zangwill instability).[8][9]
שני האפקטים הללו, שגורמים להתפתלות המדרגות, יכולים להיות קיימים בו-זמנית. התלות של החריגה בשפת המדרגה (l) תלויה בשני המקרים בקצב הגידול (Vgr) על פי חוק חזקה (אנ'): l ~ Vgr-b. החזקה (b) היא כ-0.5 עבור SESE, ורק כ‑0.25 עבור KESE. לכן, KESE שכיח יותר, כל עוד ה-ESB ב-SESE אינו גבוה מאד.
התקבצות מדרגות

כפי שראינו קודם מחסום ארליך-שוובל גורם להשוואת הרוחבים של המדרגות: כאשר יש בגרם מדרגות היורד כלפי ימין אזור עם מדרגות צרות בצפיפות גבוהה, אז קיום המחסום גורם למדרגות שמימין לאזור זה לנוע מהר יותר מאשר לאלו שמשמאלו, ורוחבי המדרגות נוטים להשתוות אלו לאלו (איור 9 פנל ימני). כאשר קיים מחסום ארליך-שוובל הפוך (האטומים מעדיפים להצטרף לשפה של המדרגה "היורדת", על פני הצטרפותם לשפת המדרגה "העולה") ההתנהגות היא, כצפוי, הפוכה: כעת המדרגות שמשמאל להפרעה נעות מהר יותר מאשר אלו שמימין, והמדרגות נהיות צפופות יותר. תופעה זו קרויה התקבצות מדרגות (step bunching). עם התפתחות הגידול המדרגות החד שכבתיות יכולות ליצור מדרגות רב-שכבתיות, שגובהן הממוצע גדול יותר ככל שמרחק הדיפוזיה של האדאטומים על פני השטח ארוך יותר.[10]

ההסבר לקיומו של מחסום ארליך-שוובל הפוך קשה יותר מאשר במקרה הרגיל. לגבי MOVPE נטען[11] שייתכן מצב שבו לפרקורסרים שנעים על הטרסות קשה להתפרק עליה. אבל, כשהם מגיעים לשפת המדרגה היורדת, הם מתפרקים יותר בקלות, מפני שיש שם יותר קשרים פתוחים. האדאטום שמשתחרר, מצטרף לשפת המדרגה שלידו, שמתחתיו, כי היא שם, ולמעשה קיים ESB שלילי (איור 10).
כשאין פירוק פרקורסרים באפיטקסיה, כמו ב-MBE, הצטרפות מועדפת של האדאטומים מהמדרגה העליונה צריכה לנבוע ממחסום ארליך-שוובל הפוך: מחסום גבוה להצטרפות אדאטום שמגיע לשפה מהמדרגה התחתונה דווקא, אך אין לכך הסבר אינטואיטיבי כמו למחסום ארליך-שוובל הרגיל.
התקבצות מדרגות שלא בגלל מחסום אנרגטי
פעמים רבות מתקבלת באפיטקסיה התקבצות מדרגות כאשר קיים במהלך הגידול חומר נוסף (זיהום). זאת, גם כאשר ללא החומר הנוסף הזה הנתונים מצביעים על קיומו של מחסום ארליך-שוובל. דוגמה לכך היא הומואפיטקסיה של יהלומי מעבדה ב-CVD בעזרת פלזמה (אנ') (PECVD): כאשר זו מבוצעת באווירה של מימן ומתאן בלבד מתקבלים פני שטח חלקים על המישור (100)[12] ומתפתחות תלוליות בצורת "עוגות חתונה".[13] אבל כשמוסיפים מעט חנקן לפאזת ההזנה מקבלים מקרו-מדרגות, שגובהן אלפי שכבות אטומיות.[12]
את התקבצות המדרגות הזו ניתן להסביר על ידי התיאוריה הקינמטית של זרימת מדרגות בגידול גבישים שפיתחו, במקביל, ניקולס קַבְּרֵרָה (אנ') וצ'ארלס פרנק (אנ') על פי משוואות הזרימה של מכוניות בכביש.[14][15] כשהמדרגות הן במרווח אחיד, הן אוספות צורני גידול בצורה אחידה, ולכן מתקדמות במהירות שווה. בדיוק כמו מכוניות שנוסעות במהירות המקסימלית המותרת בכביש. אבל אם יש על פני השטח אזור של מדרגות צפופות (בגלל חור או גל בליטוש, למשל), אז הן יכולות לאסוף רק מעט צורנים, ומתקדמות לאט. למעשה נוצר גל הלם. אבל בהמשך הוא משתטח, והמרחקים בין המדרגות, נהיים שווים. לעומת זאת, כאשר יש הפרעה קבועה על פני השטח, למשל זיהום המעכב או מונע את התקדמות המדרגות (באנלוגיה לתנועת מכוניות הפרעה קבועה היא, למשל, תאונה) הן מצטופפות יותר ויותר עד ל"פקק תנועה" אמיתי: מקרו-מדרגה. אם המדרגות יכולות מתישהו לעבור מעל הזיהום, הוא מפסיק להיות פעיל, והתנועה מתחדשת. (באנלוגיה הגיע גרר וסילק את הגרוטאות.)
תנועת המקרו-מדרגות נעצרת מפני שאדאטומים לא יכולים להצטרף אליה מלמעלה. או שהם נעצרים ליד שפת המדרגה וחוזרים חזרה, או שהם מתנדפים (דסורפציה) בחזרה לפאזת ההזנה. מלמטה, אדאטומים שמנסים "לטפס" על המצוק יוצרים מבנים תלת-ממדיים שגדלים ומתפרקים באופן אקראי. כשמבנה כזה מגיע, במקרה, לגודל קריטי, המכסה את אטומי הזיהום הסמוכים, הוא מבטל את פעילותם, ושוטף על פניהם ואותם כמו גל צונאמי, עד שהוא ניתקל ונעצר בשדה הבלימה של המזהמים הבאים; והכל מתחיל שוב. המקרו-מדרגה מתקדמת, אם כן, בקפיצות מהירות, כשהיא סוחפת איתה את המזהם באפקט צונאמי.[16]
התגברות על חוסר היציבות בגלל מחסומי ארליך-שוובל
למחסום ארליך-שוובל יכולה להיות השפעה מטיבה על הגידול באופן זרימת מדרגות (SF). עם זאת, מחסומים אלו יכולים להביא לגידול בלתי יציב כנגד כל סוג של הפרעה (זמנית או מקומית), כך שעל פני השטח מתפתחות תלוליות אם המדרגות רחבות, ובנוסף המדרגות עצמן יכולות להתפתל למבנה של "אצבעות". להתגברות על אי יציבות הגידול בגלל מחסומי ES יש, לכן, חשיבות מעשית. כדי להשיג זאת צריך ליצור מצב שבו האדאטומים מסוגלים לחלוף מעל או דרך המחסום. הדרך הפשוטה ביותר היא העלאת הטמפרטורה של הגידול, כך שלאדאטומים תהיה מספיק אנרגיה קינטית להתגבר על אנרגיית המחסום. כאשר אין אפשרות להעלות את טמפרטורת הגידול במידה הנדרשת, כדי לאפשר לאדאטומים "לחלוף" על פני מחסומי ES, אפשר לגדל בקצבי גידול נמוכים. במקרה זה אפקטים מחליקים, כמו דסורפציה, יכולים להפוך לדומיננטיים. הירידה בכמות האדאטומים יוצרת זרימה "במורד ההר" המאזנת את זו "שבמעלה ההר" בגלל מחסומי ה‑ES.
אפשרות נוספת לייצוב הגידול היא יצירת ערוץ דיפוזיה אלטרנטיבי, כך שהאדאטום "עוקף" את מחסום ES. למשל, בגידול GaN באפיטקסיית קרן מולקולרית עם ערור בפלזמה (PAMBE) מתגרענים איים על הטרסות בגלל מחסום ES גבוה. כדי למנוע אותם משתמשים בעודף גליום, כך שעל פני השטח נוצרת חד-שכבה רצופה עודפת של גליום. שכבת הגליום הזו ממסכת את מחסום ES והגידול עובר לאופן זרימת מדרגות.[17] אפשרות נוספת להתגבר על האי-יציבות בגלל מחסום ES היא שינוי הכימיה של פני השטח: בגידול GaN ב-MOVPE מתקבלות על פני השטח מדרגות מפותלות כאשר הגז הנושא הוא חנקן. לעומת זאת, אם משתמשים במימן כגז נושא מתקבלת מורפולוגיה חלקה בפני השטח. האפקט של המימן הוסבר על ידי איכול עצמי של חזית הגידול, או על ידי יצירת שכבה חלקית של מתכת ספוחה על פני השטח (בדומה לשימוש בעודף Ga בגידול ב-PAMBE).[17]
ראו גם
לקריאה נוספת
- M.A. Herman, W. Richter and H. Sitter, Epitaxy - Physical Principles and Technical Implementation Springer, Berlin, Germany, 2004, pp. 344-350, ISBN 978-3-642-08737-0
- Chaouqi Misbah, Olivier Pierre-Louis, and Yukio Saito, "Crystal surfaces in and out of equilibrium: A modern view", Reviews of Modern Physics, 82, (2010) 981. https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.82.981
הערות שוליים
- ^ G. Ehrlich and F. G. Hudda, Atomic View of Surface Self‐Diffusion: Tungsten on Tungsten, The Journal of Chemical Physics 44/3, 1966, עמ' 1039–1049
- ^ R. L. Schwoebel and E. J. Shipsey, Step Motion on Crystal Surfaces, Journal of Applied Physics 37/10, 1966, עמ' 3682–3686
- ^ R. L. Schwoebel, Step Motion on Crystal Surfaces II, Journal of Applied Physics 40/2, 1969, עמ' 614-618
- ^ J. H. Neave, P. J. Dobson, B. A. Joyce and J. Zhang, Reflection high‐energy electron diffraction oscillations from vicinal surfaces—a new approach to surface diffusion measurements, Applied Physics Letters 47/2, 1985, עמ' 100-102
- ^ J. Villain, Continuum models of crystal growth from atomic beams with and without desorption, J. Phys. I France 1, 1991, עמ' 19-42
- ^ 6.0 6.1 J. Krug, Four Lectures on the Physics of Crystal Growth, Phys. A 313, 2002, עמ' 47
- ^ W. K. Burton, N. Cabrera, and F. C. Frank, The Growth of Crystals and the Equilibrium Structure of their Surfaces, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 243, 1951, עמ' 299-358
- ^ G. S. Bales and A. Zangwill, Morphological instability of a terrace edge during step-flow growth, Physical Review B 41/9, 1990, עמ' 5000
- ^ G. S. Bales and A. Zangwill, Erratum: Morphological instability of a terrace edge during step-flow growth, Physical Review B 48/3, 1993, עמ' 2024
- ^ S. A. Chalmers, J. Y. Tsao, and A. C. Gossard, Terrace width evolution during step‐flow growth with multiterrace adatom migration, Jouranl of Applied Physics 73/11, 1993, עמ' 7351-7357
- ^ A. L.-S. Chua, E. Pelucchi, A. Rudra, B. Dwir, E. Kapon, A. Zangwill, and D. D. Vvedensky, Theory and experiment of step bunching on misoriented GaA (001) during metalorganic vapor-phase epitaxy, Applied Physics Letters 92/1, 2008, עמ' 013117
- ^ 12.0 12.1 A. Tallaire et al., Characterisation of high-quality thick single-crystal diamond grown by CVD with a low nitrogen addition, Diamond and Related Materials 15/10, 2006, עמ' 1700-1707
- ^ .V. P. Godbole et al, Evidence for layered growth of (100) textured diamond films, Applied Physics Letters 71/18, 1997, עמ' 2626-2628
- ^ R.H. Doremus, B.W. Roberts, and D. Turnbull Eds, Growth and Perfection of Crystals, New Tork: Wiley, 1958, עמ' 393-410, 411-419
- ^ A.A. Chernov, Modern Crystallography III – Crystal Growth, Berlin: Springer, 1984, עמ' 153-156
- ^ J.F Lutsko et al., Step Crowding Effects Dampen the Stochasticity of Crystal Growth Kinetics, Physical Review Letters 116, 2016, עמ' 015501
- ^ 17.0 17.1 N.A.K. Kaufmann et al., Critical impact of Ehrlich–Schwöbel barrier on GaN surface morphology during homoepitaxial growth, Journal of Crystal Growth 433, 2016, עמ' 36-42
מחסום ארליך-שוובל39220329Q4078904
