בעיית הגלריה לאמנות

בעיית הגלריה לאמנות היא בעיה תאורטית מפורסמת בתחום הגאומטריה החישובית, העוסקת במבנה של מצולעים מישוריים. הבעיה, שהוצגה בשנת 1973 על ידי המתמטיקאי ויקטור קלי, מבקשת למצוא את מספר השומרים הקטן ביותר שיוכלו, מבלי לעזוב את משמרתם, להשגיח על כל פינה בגלריה לאמנות, שקירותיה ישרים.

באופן פורמלי, נקודה A "משגיחה" על נקודה B בתוך מצולע, אם הקו הישר המחבר אותן נמצא כולו בתוך המצולע. בהינתן מצולע חסר חורים, השאלה היא מהו המספר הקטן ביותר של נקודות שכל נקודה במצולע נתונה תחת השגחתה של אחת מהן.

חסם עליון

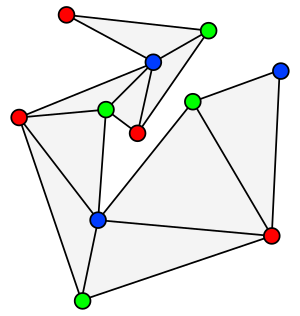
ואצלב כבטל (Václav Chvátal) הראה כי בכל מצולע ללא חורים בעל n קודקודים $\ \lfloor {\frac {n}{3}}\rfloor$ שומרים מספיקים. ההוכחה להלן מבוססת על טיעון של סטיבן פיסק. היא מסתמכת על היכולת למצוא שילוש עבור כל מצולע פשוט. השיטה היא זו: ראשית מוצאים שילוש למצולע המבוקש. אחר כך צובעים בשלושה צבעים את הקודקודים של המצולע, כך ששני קודקודים המחוברים בקו לא יהיו בעלי אותו צבע. ניתן להוכיח כי צביעה שכזו תמיד אפשרית וגם לספק אלגוריתם למציאתה (ההוכחה מבוססת על כך שהגרף הדואלי למצולע המשולש הוא בהכרח עץ, עבור מצולעים ללא חורים).

כעת בוחרים את הצבע שבו נצבע מספר הקודקודים הקטן ביותר וה"שומרים" הם הנקודות שצבועות באותו צבע.

מכיוון שקודקודי כל אחד מהמשולשים בשילוש של המצולע צבועים בכל שלושת הצבעים (כי כל שני קודקודים מחוברים בקו, ולכן אם היו שני קודקודים בעלי אותו צבע, זה היה בסתירה לדרישת הצביעה) הרי שבכל אחד מהמשולשים נמצא שומר. מכיוון שמשולש הוא צורה קמורה, די בשומר זה כדי לשמור על כל המשולש. לכן קבוצת השומרים שנבחרה מספיקה כדי לשמור על המצולע כולו.

אם למצולע $\ n$ קודקודים, הרי שמספר הנקודות שנצבעו בצבע שהופיע הכי מעט פעמים לא עולה על $\ \lfloor {\frac {n}{3}}\rfloor$ . ניתן להוכיח כי זהו חסם עליון למספר השומרים, דהיינו קיימים מצולעים שבהם נדרש כמספר הזה של שומרים.

סיבוכיות

הבעיה של מציאת המספר המינימלי של שומרים עבור מצולע מסוים (שיכול להיות קטן בהרבה מ- $\ \lfloor {\frac {n}{3}}\rfloor$ , למשל, למצולע קמור די בשומר יחיד) היא בעיה NP-קשה.