שיטת מונטה קרלו

שיטת מונטה קרלו היא שיטה לפתרון בעיות חישוביות באמצעות מספרים אקראיים (בניגוד לאלגוריתמים דטרמיניסטיים הנהוגים בדרך כלל).

אלגוריתמי מונטה קרלו הם אלגוריתמים חישוביים שמגרילים מספרים אקראיים מספר גדול של פעמים ומבצעים חישובים על המספרים שהוגרלו. לעיתים קרובות משתמשים באלגוריתמי מונטה-קרלו כדי לבצע סימולציות על מערכות פיזיקליות או מתמטיות מורכבות. השימוש העיקרי בהם הוא כדי לפתור בעיות שאינן ניתנות לפתרון מתמטי מדויק, או כדי לחסוך בכוח חישוב.

אלגוריתמים אלו מוצלחים במיוחד עבור מערכות שבהן יש הרבה דרגות חופש שתלויות אחת בשנייה, כמו בהידרודינמיקה, מבנים תאיים ובפיזיקת חלקיקים. שימוש נוסף חשוב שנעשה בהם הוא לצורך חישוב אינטגרלים רב ממדיים. זו שיטה מצוינת לחישוב של סיכונים, טובה יותר משיטות מתמטיות אחרות ומאינטואיציה אנושית.

השם "שיטות מונטה קרלו" (Monte-Carlo methods) ניתן לאלגוריתמים אלו על ידי פיזיקאים אמריקאיים במעבדה הלאומית לוס אלמוס. שם זה נובע מהטכניקה האקראית שביסוד השיטה, ומהמוניטין שיצא לקזינו של מונטה קרלו, והוא ניתן לשיטה על ידי חלוציה: הפיזיקאי אנריקו פרמי והמתמטיקאים סטניסלב אולם, ג'ון פון נוימן וניק מטרופוליס.

שיטות אקראיות לביצוע חישובים היו בשימוש עוד לפני המצאת המחשב. בשנת 1930 השתמש פרמי בשיטה כזו לחישוב תכונותיו של הנייטרון, שהתגלה באותה עת. עם זאת, המצאת המחשב, שאיפשרה ביצוע סימולציות בקלות רבה, נתנה דחיפה עיקרית לחקירתן של שיטות אלה ולהתפתחותן. בפרט, שיטות אלה שימשו בהיקף נרחב בפרויקט מנהטן לפיתוח פצצת אטום.

שיטה דומה היא שיטת לאס-וגאס שבה האלגוריתמים מניבים תמיד תוצאה נכונה, אך זמן החישוב לרוב ארוך יותר.

מבנה האלגוריתמים

ישנה קבוצה גדולה של אלגוריתמים שנמצאים בשימוש נרחב שנקראים אלגוריתמי מונטה-קרלו. לרוב האלגוריתמים האלו במבנה הבא:

מוגדר מרחב של קלטים אפשריים לאלגוריתם.
הקלטים נבחרים על ידי מחשב מתוך מרחב הקלטים האפשריים על ידי שימוש בפונקציית הסתברות מסוימת המופעלת על מרחב זה.
על קלטים אלו מחושב חישוב דטרמיניסטי מסוים.
הסטטיסטיקה של כל התוצאות נאספת ומוצגת.

הדגמה על ידי חישוב פאי

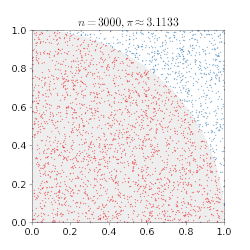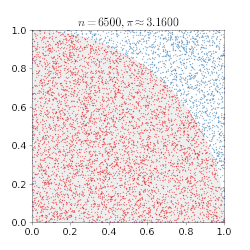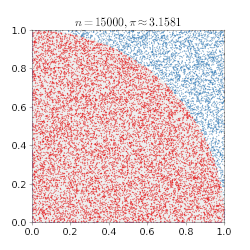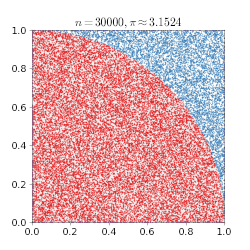
דוגמה פשוטה למימוש שיטה זו היא השיטה הבאה לחישוב π:

על לוח נצייר ריבוע שאורך צלעו שתי יחידות. נצייר מעגל חסום בריבוע - מעגל שרדיוסו שווה ליחידה אחת.
נטיל חצים לעבר הריבוע. לא נכוון את החץ למרכז הריבוע, אלא אל הריבוע כולו באופן אקראי. פונקציית ההסתברות במקרה זה היא אחידה, כלומר יש הסתברות שווה לפגיעה בכל נקודה על פני הריבוע.
כל חץ שפגע נבדק האם הוא בתוך העיגול או מחוץ לעיגול (אך בתוך הריבוע). למשל, נבדוק האם המרחק בין כל נקודת פגיעה לבין הנקודה (0,0) גדול מרדיוס המעגל, או לא. וכך נדע האם היא בתוך העיגול או מחוץ לעיגול (אך בתוך הריבוע).פעולה זו מקבילה לחישוב הדטרמיניסטי שמבוצע.
נבדוק כמה חיצים היו בתוך העיגול מתוך כמות החצים הכוללת. לאחר מספר רב של הטלות, היחס בין מספר הפעמים שהחצים פגעו בתוך המעגל, למספר הפעמים שבהם פגעו בתוך הריבוע שואף ליחס שבין שטחי שתי הצורות, שהוא 4/π . ככל שמטילים יותר חיצים, הערך של מספר החצים בתוך העיגול חלקי מספר החצים הכללי, ישאף לערך פאי חלקי ארבע. אם נכפיל את התוצאה הסופית בארבע נקבל קירוב למספר פאי.

מובן שמימוש פיזי של שיטה זו, באמצעות הטלה של חצים מוחשיים, עלול להיות מייגע. דרך מייגעת פחות תהיה כתיבת תוכנית מחשב שמבצעת סימולציה של פעולה זו.

לחישובו של π קיימות שיטות פשוטות יותר ומדויקות יותר, אך לפתרונן של בעיות חישוביות מסובכות יותר עשויה שיטת מונטה-קרלו להיות הדרך הפשוטה והמהירה לקבלת תוצאה ברמת דיוק סבירה. לשיטה זו חשיבות רבה בפיזיקה חישובית.