עץ פורש

עץ פורש (הקשתות הכחולות) של גרף הגריד

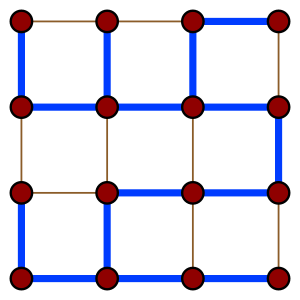
בתורת הגרפים, עץ פורש של גרף קשיר G הוא תת גרף קשיר של G, המכיל את כל צומתי G, ואין לו מעגלים. תת-גרף כזה הוא עץ.

אפשר לקבל עץ פורש על ידי הסרת קשתות מן הגרף, בזו אחר זו, כל עוד הקשירות לא נפגעת. אם הגרף כולל מעגל (כלומר, סדרה של קודקודים $\ v_{0},v_{1},\dots ,v_{n}$ שבה כל זוג קודקודים סמוכים, וכן הזוג $\ v_{0},v_{n}$, מחוברים בקשת), נוכל להסיר את אחת מקשתות המעגל בלי לפגוע בקשירות. על תהליך זה אפשר לחזור עד שבגרף אין מעגלים, והתוצאה היא עץ פורש. מכיוון שמספר הקשתות בעץ תלוי רק במספר הקודקודים שלו, לכל העצים הפורשים של אותו גרף יש אותו מספר קשתות ($\displaystyle n-1$ כאשר מספר הקודקודים בגרף הוא $\displaystyle n$). דרכים יעילות יותר למציאת עץ פורש הם באמצעות אלגוריתם חיפוש לעומק או אלגוריתם חיפוש לרוחב. אלגוריתמים אלו ירוצו בזמן ליניארי במספר הקשתות בגרף.

ספירת העצים הפורשים

את מספר העצים הפורשים של גרף אפשר לקבל ממשפט קירכהוף: אם A היא מטריצת השכנויות של הגרף ו- D המטריצה האלכסונית שרכיבי האלכסון שלה הם הדרגות של הקודקודים, אז המטריצה $\ D-A$ אינה הפיכה (שכן שורותיה מסתכמות לאפס). עם זאת, מכפלת הערכים העצמיים השונים מאפס שווה למספר העצים הפורשים, כפול במספר הקודקודים (זהו מספר העצים הפורשים, כשסופרים עצים עם שורש).

במקרה המיוחד של הגרף השלם על n קודקודים (הגרף שכל שני קודקודים שלו מחוברים בקשת אחת), מספר העצים הפורשים הוא $\ n^{n-2}$. לתוצאה זו, הקרויה נוסחת קיילי, ידועות מספר הוכחות, בהן זו של פרופר המבוססת על התאמה חד חד ערכית בין העצים הפורשים של גרף שלם לבין המילים באורך n-2 מעל אלפבית של $n$ אותיות אפשריות.

עץ פורש מינימלי

ערך מורחב – עץ פורש מינימלי

עץ פורש מינימלי

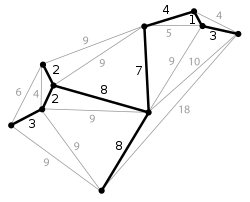
כאשר בגרף הנתון יש "משקל" לכל קשת (כלומר, זהו גרף ממושקל), טבעי לחפש עץ פורש שלו משקל כולל מינימלי. עץ כזה נקרא עץ פורש מינימלי. לבעיה של מציאת עץ כזה יש השלכות מעשיות רבות. לדוגמה, כאשר רוצים לסלול רשת כבישים בין ערים כך שיהיה מסלול בין כל שתי ערים ולעשות זאת במחיר מינימלי, מחפשים את העץ הפורש המינימלי של הגרף שצמתיו הם הערים וקשתותיו הכבישים הפוטנציאליים ביניהן (המשקל הוא אורך הכבישים שיהיה צורך לסלול).

קישורים חיצוניים

מדיה וקבצים בנושא עץ פורש בוויקישיתוף

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

23552838עץ פורש