חלון קייזר

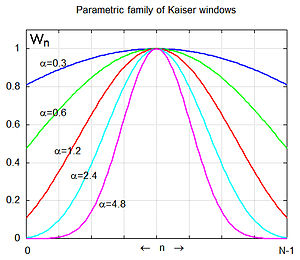
חלון קייזר (באנגלית: Kaiser Window), ידוע גם כחלון קייזר-בסל, פותח על ידי ג'יימס קייזר במעבדות בל. חלון קייזר הוא משפחה חד-פרמטרית של פונקציות חלון המשמשות לעיבוד דיגיטלי של אותות ומוגדר על ידי הנוסחה:

$w[n]=\left\{{\begin{matrix}{\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N-1}}-1\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},&0\leq n\leq N-1\\\\0&{\mbox{otherwise}},\\\end{matrix}}\right.$

כאשר:

• N הוא אורך הרצף.
• I₀ הוא סדר 0 של פונקציית בסל מהסוג הראשון.
• α מספר ממשי חיובי שרירותי אשר קובע את צורת החלון. במרחב התדירויות, הוא קובע את האיזון בין רוחב האונה הראשית ורמת האונה הצדדית. זו היא החלטה מרכזית בתכנון החלון.

כאשר N הוא מספר אי-זוגי ערך הקצה של החלון הוא  $\scriptstyle w[(N-1)/2]=1,$  וכאשר N זוגי ערכי הקצה הם  $\scriptstyle w[N/2-1]\ =\ w[N/2]\ <\ 1.$

טרנספורם פורייה

טרנספורם פורייה של חלונות קייזר עבור ערכים אופייניים של α

מאחורי הרצף הדיסקרטי עומדת הפונקציה הבאה וטרנספורם פורייה שלה:

$\underbrace {\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2t}{(N-1)T}}\right)^{2}}}\right)}{I_{0}(\pi \alpha )}} _{w_{0}(t)}\quad {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\quad \underbrace {\frac {(N-1)T\cdot \sinh \left(\pi {\sqrt {\alpha ^{2}-\left((N-1)T\cdot f\right)^{2}}}\right)}{I_{0}(\pi \alpha )\cdot \pi {\sqrt {\alpha ^{2}-\left((N-1)T\cdot f\right)^{2}}}}} _{W_{0}(f)}.$

הערך המקסימלי של (‏w₀(t הוא w₀(0) = 1. 

רצף ה-w[n] המוגדר למעלה נגזר מתוך:

$w_{0}\left(t-{\tfrac {(N-1)T}{2}}\right)\cdot \operatorname {rect} \left({\tfrac {t-(N-1)T/2}{NT}}\right),$    הנמדדים במרווחים של T,

וכאשר ()‏rect היא פונקציית המלבן האיפוס הראשון אחרי האונה של (‏W₀(f קורה ב:

$f={\frac {\sqrt {1+\alpha ^{2}}}{NT}},$

אשר ביחידות "DFT bins" הוא פשוט $\scriptstyle {\sqrt {1+\alpha ^{2}}}.$

α שולטת באיזון בין רוחב האונה הראשית ושטח האונה הצדדית. ככל ש α עולה, האונה הראשית W₀(f) גדלה ברוחב, והאונה הצדדית קטנה במשרעת. α = 0 מגיב לחלון מלבני.

עבור α גבוה, צורת חלון קייזר (הן בזמן והן בתדירות) נוטה לעקומת גאוס. חלון קייזר הוא כמעט אופטימלי במונחים של ריכוז מקסימום סביב התדירות 0 (Oppenheim et al., 1999).

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

24785398חלון קייזר