התמרת כוכב משולש
התמרת כוכב משולש היא שיטה מתמטית שנועדה לפשט את הניתוח של מעגלים חשמליים. השם התקבל מהצורה של תרשים המעגל אשר נראה כמו האות Y או האות היוונית דלתא (אות) (יוונית: Δ). התאוריה שמאחורי שיטה זו פורסמה על ידי ארתור אדווין קינלי (אנגלית: Arthur Edwin Kennelly) בשנת 1899[1] נעשה שימוש נרחב בשיטה זו בעיקר בניתוח מעגליי חשמל תלת פאזי.
התמרת כוכב בסיסית
ההתמרה משמשת להקמת מעגל חשמלי שקול למעגל בעל שלושה מסופים. כאשר שלושה רכיבים מחוברים לאותו צומת ואף אחד מהם לא משמש כמקור אז הצומת מתבטל על ידי הפיכת העכבות. בשביל קבלת שקילות, העכבה החשמלית בין כל זוג מסופים חייבת להיות זהה לשני המעגלים (לפני ההתמרה ואחרי ההתמרה). הנוסחאות הנתונות כאן נכונות הן עבור עכבות מרוכבות והן עבור עכבות ממשיות.
נוסחאות עבור התמרה מתצורת Δ לתצורת Y
הרעיון הכללי הוא לחשב את העכבה של מסוף מסוים בתצורת Y של המעגל תוך שימוש בעכבות הנתונות מתוך תצורת Δ, ולהפך. עבור עכבות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ry,R_1,R_2} עכבת מסוף y 0 היא:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_y = \frac{R_1R_2}{\sum R_\Delta}}
כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sum R_\Delta}} הוא סכום כל העכבות בתצורת Δ. בצורה מפורשת:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} R_1 &= \frac{R_bR_c}{R_a + R_b + R_c} \\ R_2 &= \frac{R_aR_c}{R_a + R_b + R_c} \\ R_3 &= \frac{R_aR_b}{R_a + R_b + R_c} \end{align}}
משוואות עבור טרנספורמציה מ Y ל Δ
הרעיון הכללי הוא לחשב את העכבה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_\Delta} בתצורת Δ על ידי הנוסחה:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_\Delta = \frac{R_P}{R_\mathrm{opposite}}}
כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rp} הוא סכום מכפלת כל זוג עכבות בתצורת Y, כלומר: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_P = R_1R_2+R_2R_3+R_3R_1} . הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_\mathrm{opposite}} הוא העכבה בתצורת ה Y בחיבור לצומת אשר אליו העכבה אותה אנחנו מעוניינים לחשב אינה מתחברת. ובצורה מפורשת:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} R_a &= \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_1} \\ R_b &= \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_2} \\ R_c &= \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_3} \end{align}}
ניתוח מעגל: שיטה לפתרון תצורת Δ על ידי המרה לתצורת Y
מעגל שיש בו שילוב של שתי התצורות המדוברות צריך להיות מומר לתצורת Y. על ידי שינוי מתוצרת Δ לתצורת Y, ניתן לנתח כל אלמנט במעגל בנפרד. שיטה זו נועדה לפשט את ניתוח המעגל. (הערה: ההתנהגות ההרמונית של המעגל המקורי נשמרת). ההמרה מתצורת Δ לתצורת Y היא כך:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} V_{\text{LL}} = \sqrt{3}V_{\text{LN}} \angle 30 \\ I_{\text{LL}} = \sqrt{3}I_{\text{LN}} \angle-30\\ Z_{\Delta}/3 = Z_{\text{Y}} \\ S_{3\Phi} = |S_{3\Phi}|= \sqrt{3}V_{\text{LL}} I_{\text{L}}=3V_{\text{LN}} I_{\text{L}}\\ \end{align}}
פישוט רשת נגדים
רשת נגדים בין שני מסופים ניתנת לפישוט לנגד שווה ערך (ובאופן כללי יותר הדבר מתקיים גם לעכבות). שיטת חיבור נגדים בטור ושיטת חיבור נגדים במקביל הן כלים בסיסיים לפישוט רשת נגדים, אך עבור רשת הנגדים המתוארת בתמונה הן לא יספיקו. ניתן לעשות שימוש בהתמרת כוכב משולש על מנת לפשט את רשת הנגדים כמתואר בתמונה.
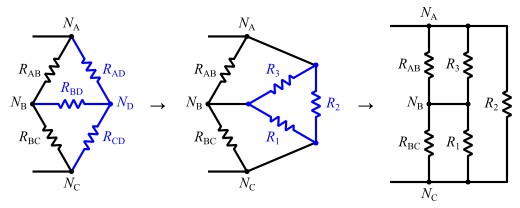
התמרת כוכב משולש ההפוכה (מתצורת Δ לתצורת Y) אשר מוסיפה צומת, נועדה גם כן על לפשט את המעגל.
הדגמה
התמרה מתצורת Δ לתצורת Y
כדי לקשר את {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_a, R_b, R_c} } מתצורת Δ ל {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1, R_2, R_3} } מתצורת Y, משווים את העכבה בין שני צמתים בתצורת Δ לעכבה המתאימה בין שני צמתים בתצורת Y, חוזרים על התהליך עבור כל זוג צמתים. העכבה בין הצמתים נקבעת כאשר הצומת האחר לא מחובר למעגל ובמקומו יש קצר. העכבה בין N_1 ו N_2 כאשר N_3 מקוצר, בתצורת Δ:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} R_\Delta(N_1, N_2) &= R_c \parallel (R_a + R_b)= \\ &= \frac{1}{\frac{1}{R_c} + \frac{1}{R_a + R_b}} \\ &= \frac{R_c(R_a + R_b)}{R_a + R_b + R_c} \end{align}}
כדי להקל על הרישום נקרא לסכום {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_T} }, {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_A, R_B, R_C} }:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_T = R_a + R_b + R_c }
לכן:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_\Delta(N_1, N_2) = \frac{R_c(R_a+R_b)}{R_T} }
העכבה המתאימה בין N_1 ו N_2 בתצורת Y, היא:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_Y(N_1, N_2) = R_1 + R_2}
נשווה בין העכבות שהתקבלו:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_Y(N_1, N_2) = R_\Delta(N_1, N_2)}
לכן מתקבל:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1+R_2 = \frac{R_c(R_a+R_b)}{R_T}} (1)
נחזור על התהליך עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R(N_2,N_3)} :
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_2+R_3 = \frac{R_a(R_b+R_c)}{R_T}} (2)
נחזור על התהליך שוב עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R(N_1,N_3)} :
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1+R_3 = \frac{R_b(R_a+R_c)}{R_T}.} (3)
מכאן ניתן לקבוע את הערכים {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1, R_2, R_3} } על ידי צירוף לינארי. למשל מחיבור משוואות (1) ו (3) וחיסור משוואה (2) נקבל:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1+R_2+R_1+R_3-R_2-R_3 = \frac{R_c(R_a+R_b)}{R_T} + \frac{R_b(R_a+R_c)}{R_T} - \frac{R_a(R_b+R_c)}{R_T} }
לכן:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1 = \frac{R_bR_c}{R_T}.}
כאשר,
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_T = R_a + R_b + R_c }
לכן מתקבל:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1 = \frac{R_bR_c}{R_T}} (4)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_2 = \frac{R_aR_c}{R_T}} (5)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_3 = \frac{R_aR_b}{R_T}} (6)
התמרה מתצורת Y לתצורת Δ
נקבע ש:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_T = R_a+R_b+R_c} .
אנחנו יכולים לכתוב את נוסחאות המעבר מתצורת Y לתוצרת Δ כך:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_T = R_a+R_b+R_c} .
ומתצורת Δ לתצורת Y כך:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1 = \frac{R_bR_c}{R_T} } (1)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_2 = \frac{R_aR_c}{R_T} } (2)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_3 = \frac{R_aR_b}{R_T} } (3)
מהכפלת כל זוג משוואות, מתקבל:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1R_2 = \frac{R_aR_bR_c^2}{R_T^2}} (4)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1R_3 = \frac{R_aR_b^2R_c}{R_T^2}} (5)
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_2R_3 = \frac{R_a^2R_bR_c}{R_T^2}} (6)
נסכום את המשוואות שהתקבלו:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1R_2 + R_1R_3 + R_2R_3 = \frac{R_aR_bR_c^2 + R_aR_b^2R_c + R_a^2R_bR_c}{R_T^2}} (7)
נוציא גורם משותף במונה {הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_aR_bR_c} }:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1R_2 + R_1R_3 + R_2R_3 = \frac{(R_aR_bR_c)(R_a+R_b+R_c)}{R_T^2}}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1R_2 + R_1R_3 + R_2R_3 = \frac{R_aR_bR_c}{R_T}} (8)
נחלק את משוואה (8) במשוואות (1),(2) ו (3) בנפרד. חלוקה במשוואה (1):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_1} = \frac{R_aR_bR_c}{R_T}\frac{R_T}{R_bR_c}}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_1} = R_a} (9)
חלוקה במשוואה (2):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_2} = \frac{R_aR_bR_c}{R_T}\frac{R_T}{R_aR_c}}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_2} = R_b} (10)
חלוקה במשוואה (3):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_3} = \frac{R_aR_bR_c}{R_T}\frac{R_T}{R_aR_b}}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R_1R_2 + R_1R_3 + R_2R_3}{R_3} = R_c,} (11)
משוואות (9), (10) ו (11) שהתקבלו מקשרות בין תצורת Y לתצורת Δ.
ראו גם
קישורים חיצוניים
- William Stevenson, Elements of Power System Analysis 3rd ed., McGraw Hill, New York, 1975, מסת"ב 0-07-061285-4
הערות שוליים
- ↑ A.E. Kennelly, "Equivalence of triangles and three-pointed stars in conducting networks", Electrical World and Engineer, vol. 34, pp. 413–414, 1899.
התמרת_כוכב_משולש19640143Q1110301