גל שן מסור
 |
יש להשלים ערך זה: בערך זה חסר תוכן מהותי.
| |
| יש להשלים ערך זה: בערך זה חסר תוכן מהותי. | |
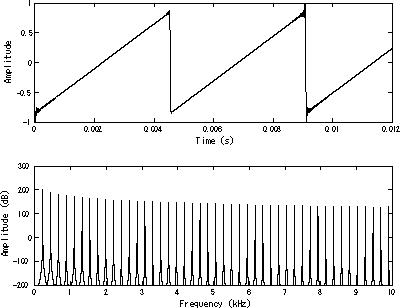
גל שן-מסור מכונה גם גל מסור (באנגלית: "Sawtooth wave") הוא גל שאינו בצורה סינוסואידלית. נקרא כך בשל הדמיון שלו לשיניים של מסור.
הקונבנציה היא שגל שן-מסור מתגבר בעצמתו עד למקסימום ואז יורד בחדות. לעומת זאת, ב-"גל שן-מסור הופכי", הגל יורד בעצמתו ואז עולה בחדות. ניתן לחשוב עליו גם כעל מקרה הקיצוני של גל משולש אסימטרי.
- $ x(t)=t-\lfloor t\rfloor =t-\operatorname {floor} (t) $
המבוססת על פונקציית הרצפה של הזמן t היא דוגמה לגל שן-מסור עם מחזור תדירות של 1.
צורה כללית יותר, בטווח 1- עד 1, עם מחזור a, היא:
$ x(t)=2\left({t \over a}-\left\lfloor {1 \over 2}+{t \over a}\right\rfloor \right)=2\left({t \over a}-\operatorname {floor} \left({1 \over 2}+{t \over a}\right)\right) $.
לפונקציית גל שן-מסור זו יש אותה פאזה כמו לפונקציית הסינוס.
גל שן-מסור ניתן לבנייה באמצעות סינתזה אדיטיבית. טור הפורייה האינסופי:
$ x_{\mathrm {reversesawtooth} }(t)={\frac {2}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}} $
מתכנס לגל שן מסור הופכי. גל שן-מסור קונבנציונלי ניתן לבנייה כך:
$ x_{\mathrm {sawtooth} }(t)={\frac {A}{2}}-{\frac {A}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kft)}{k}} $
כאשר A האמפליטודה. ניתן לראות שהמשרעת של ההרמוניה השנייה היא חצי מהמשרעת של תדר היסוד, המשרעת של ההרמוניה השלישית היא שליש מהמשרעת של תדר היסוד, וכך הלאה.
