אפקט הפרפר

מושכים נקודתיים במרחב פאזה דו ממדי

אֵפֵקְט הַפַּרְפַּר הוא ביטוי מתחום תורת הכאוס הממחיש מצב של "תלות רגישה בתנאי ההתחלה", לפיו שינויים קטנים בתנאי ההתחלה של מערכת דינאמית לא ליניארית עשויים לגרום לשינויים גדולים בהתנהגות המערכת בטווח הזמן הארוך. המונח מובא לעיתים בהקשרים איזוטריים, אך למעשה ניתן לתיאור על ידי מערכות פשוטות מאוד, לדוגמה: כדור המונח בראש גבעה עשוי להתגלגל לכל אחד מהשקעים שבפני שטח הגבעה, בתלות בשינויים הקלים בתנוחתו ההתחלתית.

הביטוי אפקט הפרפר מייצג מקרה פרטי בו משק כנפי פרפר עשוי ליצור שינויים קטנים באטמוספירה שבסופו של דבר יגרמו להופעת סופת טורנדו (או לחלופין ימנעו את הופעתה). הכנפיים המתנופפות מייצגות שינוי קטן בתנאי ההתחלה של המערכת, שגורם שרשרת מאורעות המובילים לתופעה בקנה מידה גדול. אם הפרפר לא היה מנפנף בכנפיו, ייתכן ומסלול המערכת היה שונה במידה ניכרת.

שיבה לאחור, שהיא החזרה המקורבת של המערכת לעבר תנאי ההתחלה, יחד עם התלות הרגישה בתנאי ההתחלה, הם שני הרכיבים העיקריים של תנועה כאוטית, המקשה על ניבוי התנהגותן של מערכות מורכבות, כמו למשל מזג האוויר, מעבר לטווח זמן מסוים (במקרה של מזג אוויר, מדובר בטווח של שבוע בקירוב).

היסטוריה

המצב של תלות רגישה בתנאי התחלה תואר לראשונה בספרות על ידי ז'אק אדמר ב-1890 והפך לפופולרי בספרו של פייר דוהם משנת 1906. נראה כי הרעיון שלפרפר אחד יכולה להיות השפעה כה מכרעת על מאורעות עוקבים, הופיע לראשונה ב-1952 בסיפור קצר מאת ריי ברדבורי על מסע בזמן, אף על פי שהמונח "אפקט הפרפר" עצמו קשור לעבודה מדעית של אדוארד לורנץ משנת 1963 שהגיש לאקדמיה למדעים של ניו-יורק, בה טען כי "מטאורולוג אחד העיר כי אם התאוריה נכונה, נפנוף אחד של כנפי שחף עשוי לשנות את מהלך מזג האוויר לנצח". באזכורים מאוחרים יותר העדיף לורנץ להשתמש ב"פרפר", שכן נשמע פואטי יותר מ"שחף" ומזכיר בצורתו את מושך לורנץ. לפי לורנץ, הכותרת להרצאה שלורנץ אמור לשאת בכנס ה-139 של האגודה האמריקנית להתקדמות במדעים AAAS ב-1972, "האם נפנוף כנפי פרפר בברזיל עשוי לגרום לטורנדו בטקסס?". נהגתה על ידי פיליפ מריליס ממארגני הכנס לאחר שלא הצליח ליצור קשר עם לורנץ ולשאול אותו מה הכותרת להרצאתו.

המחשה

אפקט הפרפר במושך לורנץ
זמן $0\leq t\leq 30$		קואורדינטת z
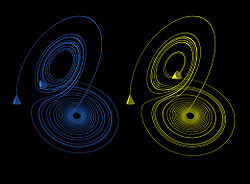
צורות אלה מראות שני מקטעים של התפתחות תלת-ממדית בשני מסלולים (אחד בכחול, השני בצהוב) לאותו פרק זמן במושך לורנץ, המתחילים בשתי נקודות התחלה הנבדלות רק ב-10-5 בציר ה-x. תחילה נראים שני המסלולים מתואמים, כפי שניכר מההבדל הקטן בין קואורדינטת z של המסלול הצהוב והכחול, אולם עבור t>23 ההבדל גדול כמו הערך של המסלול. ההבדל במצבם האחרון של הקונוסים הצהובים והכחולים מצביע על כך ששני המסלולים אינם מתואמים יותר כאשר t=30.
אנימציית Java של מושך לורנץ המראה את ההתפתחות המתמשכת.

הגדרה מתמטית

מערכת דינאמית עם מפת התפתחות $f^{T}$ מציגה תלות רגישה בתנאי ההתחלה אם נקודות קרובות באופן שרירותי הולכות ומתרחקות זו מזו ככל ש-$t$ גדל. אם $M$ הוא מרחב הרקע של המפה $f^{T}$, אזי $f^{T}$ מציגה תלות רגישה בתנאי ההתחלה אם יש $\delta >0$ כך שעבור כל נקודה $x\in M$ וכל סביבה $N$ המכילה את $x$, קיימת נקודה $y$ מהסביבה $N$ וזמן $t$ כך שהמרחק מקיים

$d(f^{\tau }(x),f^{\tau }(y))>\delta \,$

ההגדרה אינה דורשת שכל הנקודות מסביבה כלשהי יהיו נפרדות מנקודת הבסיס $x$.

מכניקת קוונטים

האפשרות לקיום אפקט הפרפר נחקרה בתחום הפיזיקה החצי קלאסית והפיזיקה הקוונטית, בתחומים של אטומים בשדות חזקים ובעיית קפלר ( מקרה פרטי של בעיית שני הגופים) [1]. קיימת מחלוקת בין החוקרים האם האפקט אכן מתקיים כאשר בין אלו הטוענים כי אפקט הפרפר מתקיים במכניקה הקוונטית ניתן למנות את דויד פאולין אשר הציג במחקרו אלגוריתם  קוונטי למדידת הקצב בו מצבים התחלתיים זהים מתפצלים כאשר הם נתונים לדינמיקה שונה במקצת, ולפיהם אפקט הפרפר הקלאסי מתייחס להשפעה של שינוי קטן במערכת המילטון עם מיקום ומהירות התחלתית נתונים. אפקט זה הוכח באופן ניסויי על מערכת פיזיקלית של בנזן

במטריצה גבישית נוזלית. [2] מנגד קיימים חוקרים אחרים הטוענים כי תאוריית המטריצה האקראית וסימולציות שונות שנעשו עם מחשבים קוונטים מוכיחים כי חלקים מאפקט הפרפר אינם מתקיימים במכניקה הקוונטית, לדוגמה מחקרם של בין יאן וניקולאי סינתסין המראה כי ניתן לשחזר מידע למצבו ההתחלתי אשר היה ניראה כי סדרו נפגע באופן כאוטי וזאת על ידי פרוטוקול היפוך זמן . [3]

---

[1] Heller, Eric J.; Tomsovic, Steven (1993). Postmodern Quantum Mechanics. Physics Today, 46(7), 38–. doi:10.1063/1.881358

[2] Lee, Jae-Seung; Khitrin, A. K. (2004). Quantum amplifier: Measurement with entangled spins. The Journal of Chemical Physics, 121(9), 3949–. doi:10.1063/1.1788661

[3] Yan, Bin; Sinitsyn, Nikolai A. (2020). Recovery of Damaged Information and the Out-of-Time-Ordered Correlators. Physical Review Letters, 125(4), 040605–. doi:10.1103/PhysRevLett.125.040605

אזכורים בתרבות הפופולרית

בתרבות הפופולרית העוסקת במסע בזמן נעשה שימוש רב ברעיון שמאחורי אפקט הפרפר, אך לרוב באופן לא מדויק. רוב תיאורי המסע בזמן כושלים בהתייחסות לאפקט הפרפר, שכן לפי התאוריה האמיתית, אם ההיסטוריה הייתה אכן יכולה "להשתנות", די בעצם הנוכחות של נוסעים בזמן בעבר על מנת לשנות מאורעות בטווח הזמן הקצר (כגון מזג האוויר), ותהיה לה השפעה בלתי ניתנת לניבוי על העתיד הרחוק, כך שלא ייתכן שמי שנסע לעבר יוכל לחזור לאותה גרסת מציאות שממנה הגיע.

בעקבות הקורונה

בעקבות נגיף הקורונה ישנם אנשים שהמציאו שם חדש לאפקט הפרפר: 'אפקט העטלף' (ראה קישור בקישורים חיצוניים)

ראו גם

• דטרמיניזם
• אפקט הדומינו
• מדרון חלקלק
• אפקט הפרפר (סרט)
• הכול בגלל מסמר

לקריאה נוספת

• ג'יימס גליק, כאוס, ספרית מעריב, 1991

קישורים חיצוניים

• אפקט הפרפר (שעשועים מתמטיים)
• מכנפי פרפר לאימייל יחיד (אוניברסיטת קורנל)
• אפקט הפרפר באתר מכון ניו-אינגלנד למערכות מורכבות
• The Chaos Hypertextbook הקדמה על תורת הכאוס ופרקטלים
• שחר שילוח, אפקט הפרפר: מה המשמעות האמיתית של הביטוי הכל כך שגור הזה?, באתר nrg‏, 20 ביוני 2008
• אפקט הפרפר, באתר MathWorld (באנגלית)
• אפקט הפרפר פנחס יחזקאלי - היבטים פוליטיים
• ד"ר אסף רוזנטל, ‏אפקט הפרפר – במציאות, באתר "הידען", 4 באוגוסט 2019
• אפקט העטלף - מקור
• אפקט הפרפר במכניקת קוונטים

הערות שוליים

• Robert L. Devaney (2003). Introduction to Chaotic Dynamical Systems. Westview Press. מסת"ב 0-8133-4085-3.
• Robert C. Hilborn (2004). Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics. American Journal of Physics. Vol. 72. pp. 425–427.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

34213047אפקט הפרפר