אלגוריתם לויד-מקס

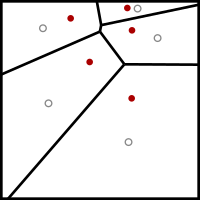
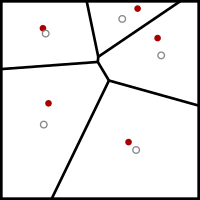
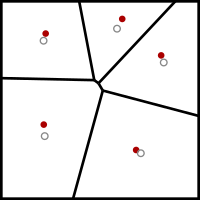
אלגוריתם לויד- מקס הוא אלגוריתם המאפשר למזער את השגיאה הריבועית הממוצעת בקוונטיזציה.

קוונטיזציה אחידה ושגיאת קוונטיזציה

בקוונטיזציה אחידה, בהינתן N, מספר הרמות שאליהן אנו מחלקים את הטווח, מספיק לקבוע את רמת הקוונטיזציה הראשונה ואת ההפרש בין הרמות, וכך הקוונטיזציה נקבעת חד חד ערכית. אולם, הדבר מגביל אותנו מבחינת שגיאת הקוונטיזציה אותה ניתן להשיג. נרצה להשיג חופש גדול יותר בבחירת מדרגות הקוונטיזציה וערכיהן בשביל לקבל שגיאה נמוכה יותר.

$\mathrm {MSE} =\int \limits _{-\infty }^{a1}(x-x_{1})^{2}f_{x}(x)dx+\textstyle \sum _{i=2}^{N}\int \limits _{a_{i-2}}^{a_{i}}(x-x_{i})^{2}f_{x}(x)dx+\int \limits _{a_{N-1}}^{\infty }(x-x_{N})^{2}f_{x}(x)dx+\textstyle \displaystyle$

נחשב את $x_{i}$ ו- $a_{i}$ האופטימליים:

עבור $a_{i}$ , נגזור ונשווה ל-0:

${dMSE \over da_{i}}=f_{x}(a_{i})[(a_{i}-x_{i})^{2}-(a_{i}-x_{i+1})^{2}]=0$

(שכן, ${d \over db}\int \limits _{a}^{b}g(x)dx=g(b),\qquad {d \over da}\int \limits _{a}^{b}g(x)dx=g(a)$ )

ואזי, נקבל $a_{i}$ האופטימלי:

$a_{i}={x_{i}+x_{i+2} \over 2}$

עבור $x_{i}$ , נגזור ונשווה ל-0:

${dMSE \over da_{i}}=2\int \limits _{a_{i-1}}^{a_{i}}(x_{i}-x)f_{x}(x)dx=0$

$x_{i}\int \limits _{a_{i-1}}^{a_{i}}f(x)dx=\int \limits _{a_{i-1}}^{a_{i}}xf(x)dx$

ואזי, נקבל $x_{i}$ האופטימלי:

$x_{i}={\int \limits _{R_{i}}xf(x)dx \over \int \limits _{R_{i}}f(x)dx}$

כאשר: $R_{i}\in \left\{{a_{i-1}},{a_{i}}\right\}$

אלגוריתם Lloyd- Max

- קבע בצורה שרירותית ואחידה את $R_{i}$ עבור $i=1,...,N$ .

- בצע בצורה איטרטיבית עד התכנסות:

$x_{i}=\int \limits _{R_{i}}xf(x)dx/\int \limits _{R_{i}}f(x)dx,\qquad i=1,...,N$
$a_{i}={x_{i}+x_{i+2} \over 2},\qquad i=1,...,N$

לא בהכרח מתכנס למינימום מוחלט (יכולים להיתקע במינימום מקומי)
כאמור, אלגוריתם זה נותן קוונטיזציה $(a_{i},x_{i})$
ישנן טבלאות עבור התפלגות גאוסית $N(0,1)$ $N(0,1)$ עבור ערכי N שונים.
- במקרים שהתוחלת היא $\mu$ , אזי: ${\widehat {a_{i}}}=a_{i}+\mu \qquad {\widehat {x_{i}}}=x_{i}+\mu$
- ובמקרים שהשונות היא $\sigma ^{2}$ , אזי: ${\widehat {a_{i}}}=a_{i}\sigma \qquad {\widehat {x_{i}}}=x_{i}\sigma$
- ובמקרה הכללי: ${\widehat {a_{i}}}=a_{i}\sigma +\mu \qquad {\widehat {x_{i}}}=x_{i}\sigma +\mu \qquad {\widehat {MSE}}=\sigma ^{2}\cdot MSE$