מרחק המינג

לכל שני קודקודים מחוברים בתמונה, מרחק המינג 1. מרחק המינג בין המחרוזת 0100 למחרוזת 1001 הוא 3 (מספר הצלעות במסלול האדום).

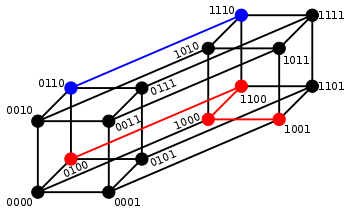
בתורת האינפורמציה, מרחק הַמינג (Hamming) בין שתי מחרוזות בעלות אורך זהה, הוא מספר המקומות שבהם סימנים מקבילים בשתי המחרוזות שונים זה מזה. בניסוח אחר, מרחק המינג הוא מספר השינויים המזערי שיש לעשות במחרוזת אחת כדי לקבל את המחרוזת השנייה. כן ניתן לראות את מרחק המינג כאילו נוצר בעת שידור המחרוזת הראשונה, שנקלט כמחרוזת השנייה, כך שמרחק המינג מייצג את מספר השגיאות שנוצרו בתשדורת זו. מחרוזת, לעניין זה, יכולה להיות בכל שיטת קידוד, כגון מחרוזת סיביות, מחרוזת תווים וכדומה. דוגמאות:

• מרחק המינג בין המחרוזת 1011101 למחרוזת 1001001 הוא 2.
• מרחק המינג בין המחרוזת 2143896 למחרוזת 2233796 הוא 3.
• מרחק המינג בין המחרוזת "toned" למחרוזת "roses" הוא 3.

משקל המינג של מחרוזת הוא מרחק המינג שלה ממחרוזת בעלת אותו אורך שכולה אפסים. למעשה זהו מספר הסימנים שאינם אפס. במחרוזת סיביות זהו מספר הסיביות שערכן 1. דוגמה: משקל המינג של המחרוזת 11101 הוא 4.

מרחק המינג קרוי על שמו של ריצ'רד המינג, שהציג רעיון זה במאמרו הבסיסי error-detecting and error-correcting codes משנת 1950, מאמר שבו הציע את קוד המינג.

מאפיינים

לאורך קבוע n, מרחק המינג הוא מטריקה מעל קבוצת המילים בנות אורך זה: קל לראות שמתקיימות הדרישות לאי-שליליות, למרחק 0 בין שווים ולסימטריה, ובאמצעות אינדוקציה שלמה ניתן להוכיח שמתקיים אי שוויון המשולש.

את מרחק המינג בין שתי מחרוזות ניתן לראות גם כהפרש ביניהן, על-פי הגדרה נאותה של פעולת החיסור. לשתי מחרוזות בינאריות ההפרש הוא מספר הביטים הדלוקים בתוצאה של פעולת XOR ביניהן, או מספר הביטים הדלוקים לאחר חיסור רגיל במרחב הווקטורי $\mathbb {Z} _{2}^{n}$ כאשר מזהים את התו 0 עם המספר 0 (מודולו 2) ואת התו 1 עם הספרה 1 (מודולו 2).

ראו גם

• סאונדקס
• מרחק לוינשטיין

לקריאה נוספת

• Hamming, Richard W. (1950). "Error detecting and error correcting codes" (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. MR 0035935.
• Pilcher, C. D.; Wong, J. K.; Pillai, S. K. (במרץ 2008). "Inferring HIV transmission dynamics from phylogenetic sequence relationships". PLoS Med. 5 (3): e69. doi:10.1371/journal.pmed.0050069. PMC 2267810. PMID 18351799. {{cite journal}}: (עזרה)
• Wegner, Peter (1960). "A technique for counting ones in a binary computer". Communications of the ACM. 3 (5): 322. doi:10.1145/367236.367286.
• Ayala, Jose (2012). Fast Propagation of Hamming and Signal Distances for Register-Transfer Level Datapaths. Integrated Circuit and System Design. Vol. 1. p. 62.
• MacKay, David J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32715161מרחק המינג